Java数组的几种常用操作方法(排序算法及查找)
查找是在数组中寻找特定元素的过程。
线性查找法
线性查找法将要查找的关键字key与数组中的元素逐个进行比较。如果匹配成功,线性查找法则返回与关键字匹配的元素在数组中的下标;如果没有匹配成功,则返回-1。下面给出线性查找法的程序:
private static int LinearSearch(int[] list,int key) {
// TODO Auto-generated method stub
for(int i = 0;i < list.length;i++){
if(key == list[i]){
return i;
}
}
return -1;
}int[] list = {1,3,5,7,-3};
int number1 = LinearSearch(list,1);
int number2 = LinearSearch(list,7);
int number3 = LinearSearch(list, -5);
System.out.println(number1);
System.out.println(number2);
System.out.println(number3);输出结果:
0
3
-1线性查找法把关键字和数组中的每一个元素进行比较,这种算法平均来看,得和数组中一半的元素进行比较,因此效率不高。
二分查找法
二分法是另一种常见的对数组列表的查找方法。使用二分查找法的前提条件是数组中的元素必须先排好序。
二分查找法首先将关键字与数组的中间元素进行比较,每次比较之后就排除掉一半的数组元素。对于一个有1024个元素的数组,在最坏的情况下,二分查找法只需要比较log2n + 1= 11次,而在最坏的情况下线性查找要比较1023次。
下面给出二分法查找的程序:
private static int binarySearch(int[] list,int key) {
// TODO Auto-generated method stub
int low = 0;
int high = list.length - 1;
//直到low>high时还没找到关键字就结束查找,返回-1
while(low<=high){
int mid = (low+high)/2;
if(key < list[mid]){
high = mid - 1;
}
else if(key > list[mid]){
low = mid + 1;
}
else if(key == list[mid]){
return mid;
}
}
return -1;
}
用下面的语句跟踪该方法
int[] list = {1,3,5,7,9,10,34,56,78,99};
int number1 = binarySearch(list,7);
int number2 = binarySearch(list,34);
int number3 = binarySearch(list,100);
System.out.println(number1);
System.out.println(number2);
System.out.println(number3);输出结果:
3
6
-1输出的只是关键字的下标。
二分法效率比线性查找高,但是要求数组先排好序。下面我们看数组的排序。
像查找一样,排序也是计算机中常用的操作。这里介绍两种方法。
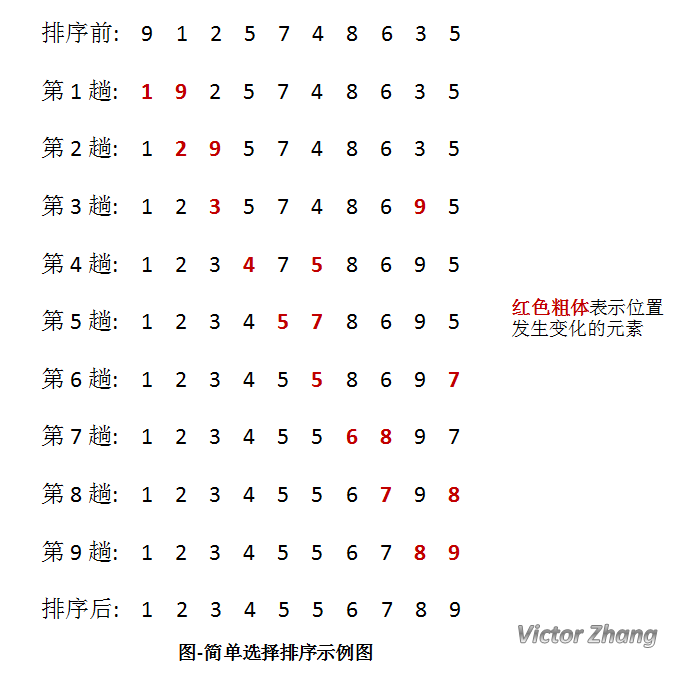
选择排序
假设要按升序排列一个数组。选择排序法先找到数列中最小的数,然后将它放在数列中的最前面。接下来再剩下的数中选择最小数,将它放在第一个的后面,以此类推,直到数列中仅剩一个数为止。
看一张示例图,会讲解得更清楚:
下面显示了选择排序的程序:
public static int[] SelectionSort(int[] arrays){
//i表示交换的次数,从上面的图中就可以发现交换9次
for (int i = 0; i < arrays.length - 1; i++) {
int temp = 0;//用来保存最小的那个数
int index = i; // 用来保存最小值的索引
// 寻找第i个小的数值
//这一次循环之后,index将获得最小值的索引
for (int j = i + 1; j < arrays.length; j++) {
if (arrays[index] > arrays[j]) {
index = j;
}
}
// 交换位置,将找到的第i个小的数值放在第i个位置上
//将最小值赋值给temp
temp = arrays[index];
arrays[index] = arrays[i];
arrays[i] = temp;
}
return arrays;
}
用下面的语句跟踪该方法
int[] list = {3,5,23,45,1,66};
int[] list2 = SelectionSort(list);
System.out.println(Arrays.toString(list2));输出结果:
[1, 3, 5, 23, 45, 66]eg: 我们也可以用Python来编写程序获得同样的结果:
- 编写一个用于找出数组中最小元素的函数findSmallest
def findSmallest(arr):
smallest = arr[0] <-------- 存储最小的值
smallest_index = 0 <-------- 存储最小值的索引
for i in range(1, len(arr)):
if arr[i] < smallest:
smallest = arr[i]
smallest_index = i
return smallest_indexdef selectionSort(arr): <--------- 对数组进行排序
newArr = []
for i in range(len(arr)):
smallest = findSmallest(arr) <--------- 找出数组中最小的元素,将找到的最小元素弹出数组,
并将其加入到新数组中
newArr.append(arr.pop(smallest))
return newArr
print selectionSort([5, 3, 6, 2, 10])插入排序
假设希望对一个数列进行递增排序。插入排序法的算法是在已排好序的子数列中反复插入一个新元素来对数列值进行排序的。
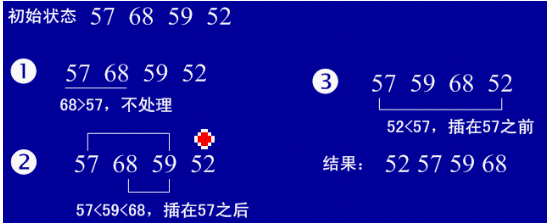
下面展示了运用插入排序算法对数列{2,9,5,4,8,1,6}进行排序:
private static int[] InsertionSort(int[] list) {
// TODO Auto-generated method stub
// 第1个数肯定是有序的,从第2个数开始遍历,依次插入有序序列
for(int i = 1;i < list.length;i++){
// 取出第i个数,和前i-1个数比较后,插入合适位置
int currentElement = list[i];
int j;
// 因为前i-1个数都是从小到大的有序序列,所以只要当前比较的数(list[j])是否比currentElement大,就把这个数后移一位
for(j = i-1;j >= 0&& list[j] > currentElement;j--){
list[j+1] = list[j];
}
list[j + 1] = currentElement;
}
return list;
}用下面的语句跟踪该方法:
int[] list = {2,9,5,4,8,1,6,-5};
int[] list2 = InsertionSort(list);
System.out.println(Arrays.toString(list2));
输出结果:
[-5,1, 2, 4, 5, 6, 8, 9]
注意:
在待排数据基本有序的情况下,直接插入排序方法是效果最好。
选择排序、堆排、归并、基数算法的时间复杂度与初始排序无关
n个·字符最坏的情况下至少需要n-1次的两两交换才能排好序
冒泡排序
在每次遍历数组中,对相邻的两个元素进行比较。如果这一对元素是降序,则交换他们的值;否则,保持值不变。
看一个示例图,有时候图解比文字更清楚:
下面展示了运用冒泡排序算法对数列{2,9,5,4,8,1,6}进行排序:
public static double[] bubbleSort(double[] arrays){
int temp;
//这里i表示交换的几次,比如上面图中52换到第一位一共进行了三次交换
for(int i = 0;i<arrays.length-1;i++){
//从后向前依次的比较相邻两个数的大小,遍历一次后,把数组中第i小的数放在第j个位置上
//这里j表示交换后它所处的位置,比如,第一次j=3,是因为52跟59交换之后到了3这个位置
//把最后一个数跟前面的数进行比较,一直到i的位置停止
for(int j = arrays.length-1;j>i;j--){
//对相邻的两个数进行比较并交换位置
if (arrays[j - 1] > arrays[j]) {
temp = arrays[j - 1];
arrays[j - 1] = arrays[j];
arrays[j] = temp;
}
}
}
return arrays;
}用下面语句跟踪上述算法:
double[] myList = {5.0, 4.4, 1.9, 2.9, 3.4, 2.9, 3.5};
double []list = bubbleSort(myList);
System.out.println("My list after sort is: " + Arrays.toString(list));输出结果:
My list after sort is: [1.9, 2.9, 2.9, 3.4, 3.5, 4.4, 5.0]快速排序
快速排序是交换类的排序,比如在站队的时候,老师说:“第一个同学出列,其他同学以第一个同学为中心,比他矮的全排在左边,比他高的全排在右边。”这就是一趟快速排序。可以看出,一趟快速排序是以一个“枢轴”为中心,将序列分成两个部分,枢轴的一边全是比它小(或者小于等于)的,另一边则全是比它大(或者大于等于)的。
快速排序算法采用了一种分治的策略,通常称其为分治法,其基本思想是:
- 1、先从数列中取出一个数作为基准数;
- 2、分区过程,将比这个数大的数全放到它的右边,小于或等于它的数全放到它的左边;
- 3、再对左右区间重复第二步,直到各区间只有一个数。
以一个简单的数组为例,我们来看一下,快速排序算法的排序过程:
再对array[0…1]和array[3..4]重复上述操作步骤就行了。
注意:在一次查找中只有i和j的值在变,X的值是一直保持不变的。
以上步骤总结为:
1、i=l,j=r,x=array[i]; 2、j- -从后向前找小于等于x的数,找到后用array[j]替代array[i]; 3、i++从前向后找大于x的数,找到后用array[i]替代array[j]; 4、一直重复执行2、3步骤,直到i=j为止,最后将基准数写入array[i]。
下面展示了如何运用快速排序算法对数组[2,7,9,3,5,6,1,8]进行排序:
private static int[] quickSortMethod(int[] array, int left, int right) {
// TODO Auto-generated method stub
if(left<right){
int i = left;//左节点,数组第一个数的索引
int j = right;//右节点,数组最后一个数的索引
int x = array[i]; //x为基准数/枢轴,一切以基准数做比较标准
//做一个循环,当i=j的时候,将基准数写入array[i]
while(i<j){
//循环从右到左找小于等于x的数,找到则右节点向前移动一位
while(i<j&&array[j]>=x){
j--;
}
//将对应索引的数赋值给左节点对应的数,注意不是赋值给x,x是不变的,左节点前移一位
if(i<j){
array[i] = array[j];
i++;
}
//循环从左到右找大于或等于x的数,找到则左节点向前移动一位
while(i<j&&array[i]<x){
i++;
}
//将对应索引的数赋值给右节点对应的数,注意不是赋值给x,x是不变的,右节点前移一位
if(i<j){
array[j] = array[i];
j--;
}
}
//将基准数填入到i
array[i] = x;
//递归分别对基准数左右两边进行排序
quickSortMethod(array, left, i-1);
quickSortMethod(array, i+1, right);
}
return array;
}用下面语句跟踪上述算法:
int[] array = {2,7,9,3,5,6,1,8};
int left = 0;
int right = array.length-1;
int[] list = quickSortMethod(array,left,right);
System.out.println(Arrays.toString(list));输出结果:
[1, 2, 3, 5, 6, 7, 8, 9]
希尔排序
希尔(Shell)排序又称为缩小增量排序,它是一种插入排序。它是直接插入排序算法的一种威力加强版。
该方法因DL.Shell于1959年提出而得名。
希尔排序的基本思想是:
把记录按步长 gap 分组,对每组记录采用直接插入排序方法进行排序。
随着步长逐渐减小,所分成的组包含的记录越来越多,当步长的值减小到 1 时,整个数据合成为一组,构成一组有序记录,则完成排序。
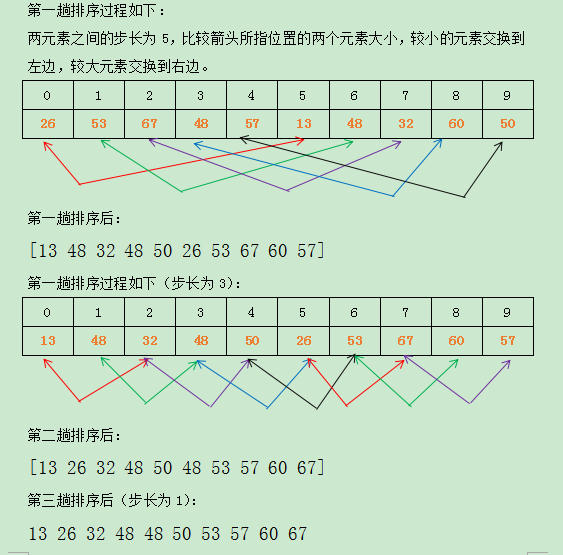
以一个简单的数组为例,我们来看一下,希尔排序算法的排序过程:
以数组{26, 53, 67, 48, 57, 13, 48, 32, 60, 50 }为例,步长序列为{5,2,1}
初始化关键字: [26, 53, 67, 48, 57, 13, 48, 32, 60, 50 ]
步长gap一般为数组长度的二分之一;
最后的排序结果:
13 26 32 48 48 50 53 57 60 67
希尔排序基本算法实现如下:
private static int[] ShellSort(int[] array) {
// TODO Auto-generated method stub
int temp = 0;
int j;
//步长gap,步长会经历三次变化,10/2=5、5/2=2、2/2=1
//增量序列的最后一个增量值必须等于1才行,
//在这个例子中表明数组将会经过三趟排序过程,这就是第一个循环的作用
//将相隔距离为gap即为5的元素组成一组,可以分为 5 组
for(int gap = array.length/2;gap>0;gap/=2){
//按照直接插入排序的方法对每个组进行排序。
//遍历从下标为gap的值的地方到最后一个值
for(int i = gap;i<array.length;i++){
//记录每一次下标为gap的值
temp = array[i];
//遍历从下标为0的值的地方到下标为gap的值
for(j = i-gap;j>=0;j-=gap){
//直接插入排序。比较两者的值,然后将较小的和较大的交换位置
if(temp<array[j]){
array[j+gap] = array[j];
}
else {
break;
}
}
array[j+gap] = temp;
}
}
return array;
}
用下面语句跟踪上述算法:
int[] array = {9, 1, 2, 5, 7, 4, 8, 6, 3, 5};
int[] list = ShellSort(array);
System.out.println(Arrays.toString(list));输出结果:
[1, 2, 3, 4, 5, 5, 6, 7, 8, 9]首先对二维数组按行排序,然后按列排序。例如数组:
{ { 4, 2 }, { 1, 7 }, { 4, 5 }, { 1, 2 }, { 1, 1 }, { 4, 1 } }
package com.example.exercise7_4;
import java.util.Arrays;
import java.util.Scanner;
public class Exercise2 {
public static void main(String[] args) {
int[][] array = { { 4, 2 }, { 1, 7 }, { 4, 5 }, { 1, 2 }, { 1, 1 }, { 4, 1 } };
sort(array);
printArray(array);
}
private static void sort(int[][] array) {
// TODO Auto-generated method stub
for(int i = 0;i < array.length;i++){
double currentMix = array[i][0];
//声明一个变量记录是哪一行
int currentMixIndex = i;
for(int j = i;j < array.length;j++){
if(currentMix > array[j][0] || currentMix == array[j][0]
&& array[currentMixIndex][1] > array[j][1]){
currentMix = array[j][0];
currentMixIndex = j;
}
}
// Swap list[i] with list[currentMinIndex] if necessary;
if (currentMixIndex != i) {
int temp0 = array[currentMixIndex][0];
int temp1 = array[currentMixIndex][1];
array[currentMixIndex][0] = array[i][0];
array[currentMixIndex][1] = array[i][1];
array[i][0] = temp0;
array[i][1] = temp1;
}
}
}
private static void printArray(int[][] array) {
// TODO Auto-generated method stub
for (int i = 0; i < array.length; i++) {
System.out.println(array[i][0] + ", " + array[i][1]);
}
}
}
- 上一篇: 我的shiro之旅: 四 自定义filter
- 下一篇: c语言下汉字转换(字符串改为utf-8编码)