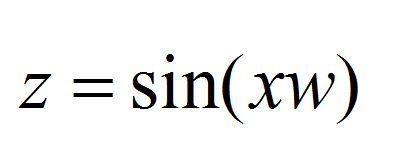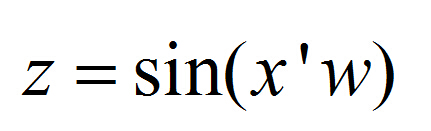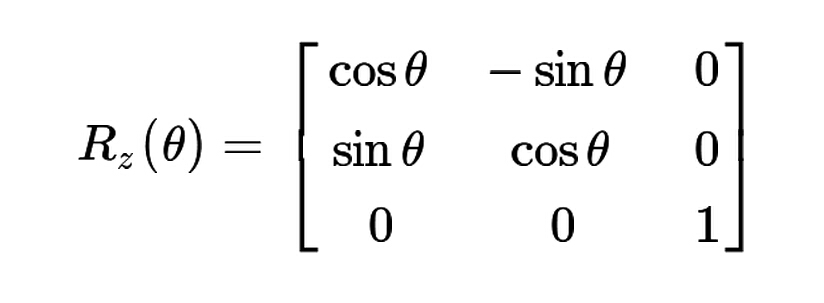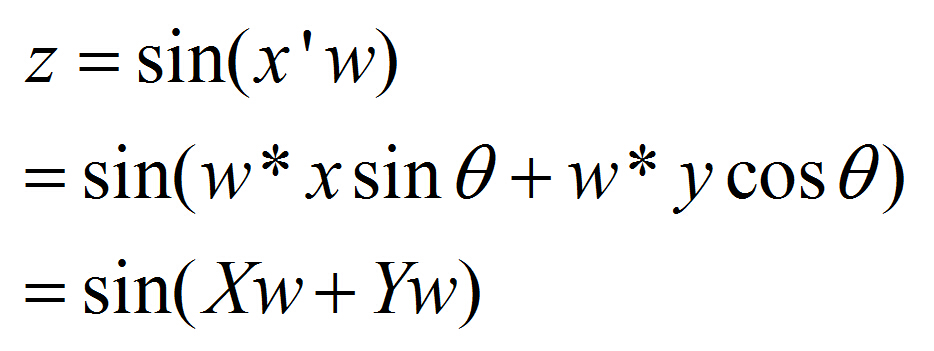OpenCV17(图像二维频谱的理解,傅里叶频谱分析)
傅里叶变换的理解参考教程:http://blog.jobbole.com/70549/
这个已经说得很详细了。
不过这个说明只是针对一维的傅里叶变换,在图像处理中我们最常见的还是二维频谱,二维频谱到底该怎么看呢?以下是我的理解,谢谢某人的帮助。
I = imread("cell.tif");
fI = fft2(I);
sfI = fftshift(fI);
temp = log(1+abs(sfI));
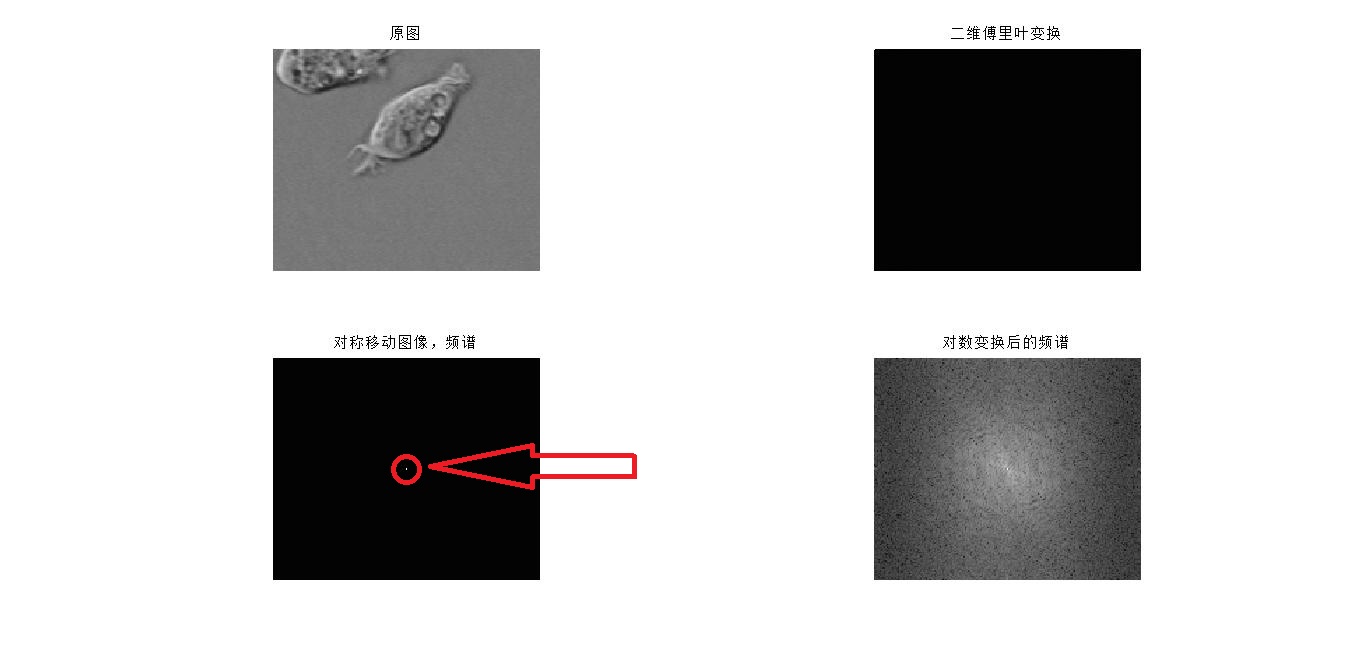
subplot(2,2,1),imshow(I),title("原图");
subplot(2,2,2),imshow(fI,[]),title("二维傅里叶变换");
subplot(2,2,3),imshow(sfI,[]),title("对称移动图像,频谱");
subplot(2,2,4),imshow(temp,[]),title("对数变换后的频谱");
cell.tif是MATLAB自带的图,结果如下:
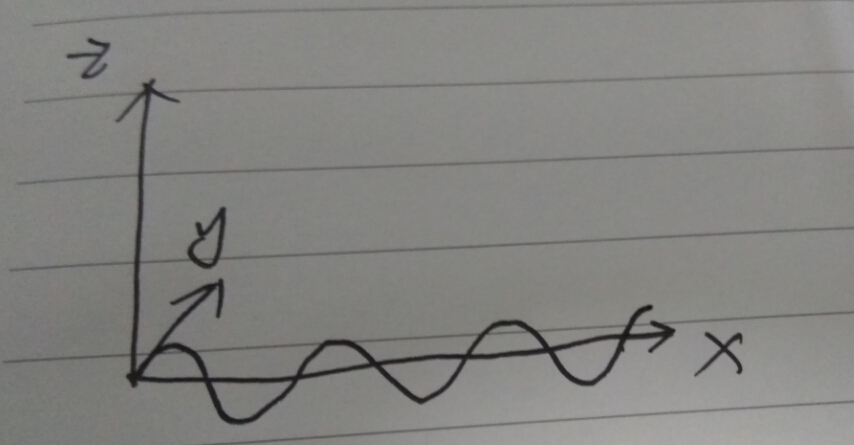
我们知道矩形波可以看作是有无数的不同相位和幅值的正弦函数组成,类似的,一个任意的平面波也可以看成是特定的某几种正弦波的组合。如图所示
(《数字图像处理与机器视觉:Visual C++与Matlab实现》P183)
(a)图上的“JC”的亮度不同,将其亮度作为纵坐标,于是得到图(b)。图(b)可以看作是图(c)中的某几个正弦平面波的组合,注意,正弦平面波的相角、幅值、传播方向都可以是不同的。
想象有一个正弦平面波(书上原话,有点迷惑人,不是平面,是曲面其实),x向传播,y的正负半轴都是曲面区域。
得正弦平面波的方程为下式,w是相位,设相角为零
从z轴往下看去,得
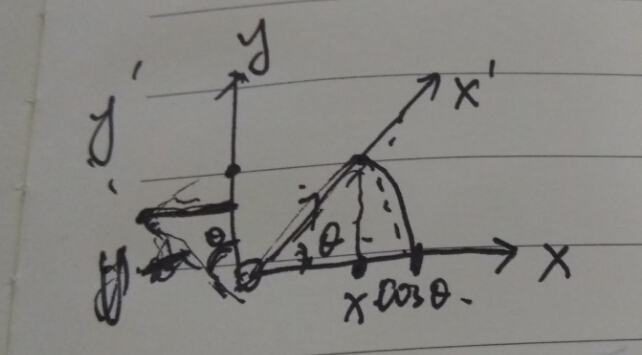
绕z轴旋转坐标系,得新坐标系(x",y")
注意,这步是为了推倒 x" 方向上的正弦平面波的方程。可知,这时候的正弦平面波方程为
沿z轴旋转 theta 角度 的旋转矩阵是
所以得下式(这步计算不明白没关系,只要知道这个矩阵可以表示两个坐标的转化关系即可,会用就行)
所以就等到,旋转之后的正弦平面波的方程可以表示为
结论!!
其实这一堆只是为找到一般正弦平面波的方程,有什么用呢?有点用。
频谱的中心为低频,外围是高频成分
可以将频谱的中心看做坐标原点,横轴为x轴,纵轴是y轴,建立坐标系。
频谱平面上的坐标(X,Y)的黑白,表示图像是否含有z = sin(Xw + Yw)这个正弦平面波成分,白即是有含有。
这里就要再注意一个问题,这里提到的频谱是频谱图的图3,再看一下频谱图,就是那个有圈圈的
是不是有点乱,所以最后我们来说明这几张图都是怎么来的。
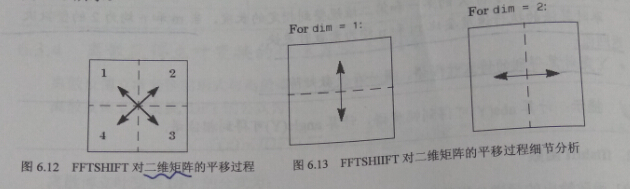
fft2之后,结果是图2,这是原始的频谱,但是由于计算中,高频在中间,低频在外围,所以不好看。
fftshift之后,做了以下对称变换,将低频调整到中间,高频在外围。注意图3中心的亮点。这表示原图中的低频成分比较多,也就是说图像的灰度变化不大,没有大的梯度值
由于图3的对比度不高,看不清楚,所以才出现了最常见到的频谱,图4
对数变换log(1+abs(XXX)),这样就看的清楚些了。
Bingo!