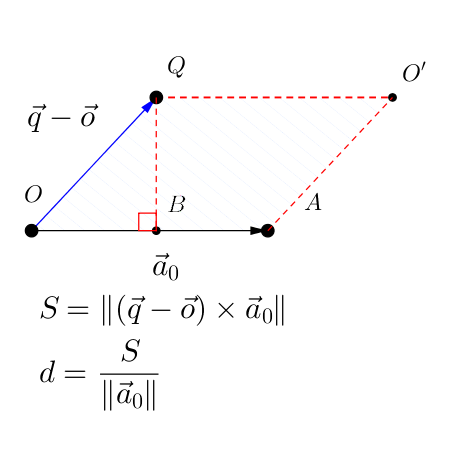
三维空间里点到直线的距离

使用叉积的表示方法

直线用固定点O$O$对应的向量 o⃗ $vec o$ 和直行的方向单位向量 a⃗ 0$vec a_0$ 表示；任意点 Q$Q$ 对应的向量 q⃗ $vec q$。 则利用向量叉积或外积的几何意义，外积的模等于两个向量为邻边的平行四边形的面积，从而可以得到三维空间点到直线的距离公式。

所用到的叉积或外积，仅在三维空间有定义，所以，适用范围也仅限三维空间。因为点和直线没有在上关系时恰好唯一确定一个平面，所以，图示可以仅用二维图表示。

http://mathworld.wolfram.com/Point-LineDistance3-Dimensional.html

叉积的定义方法，

最舒服的应该是：
a×b=[a]×b=⎡⎣⎢0a3−a2−a30a1a2−a10⎤⎦⎥⎡⎣⎢b1b2b3⎤⎦⎥ $$mathbf{a} imes mathbf{b} = [mathbf{a}]_{ imes} mathbf{b} = egin{bmatrix},0&!-a_3&,,a_2\ ,,a_3&0&!-a_1\-a_2&,,a_1&,0end{bmatrix}egin{bmatrix}b_1\b_2\b_3end{bmatrix}$$

其中一个关键的反对称矩阵的定义是这样的：
[a]×=def⎡⎣⎢0a3−a2−a30a1a2−a10⎤⎦⎥ $$[mathbf{a}]_{ imes} stackrel{ m def}{=} egin{bmatrix},,0&!-a_3&,,,a_2\,,,a_3&0&!-a_1\!-a_2&,,a_1&,,0end{bmatrix}$$
这个表示方法在计算机视觉的针孔相机标定中有特殊重要的地位。

我感觉这个表示方法比常见的如下的计算行列式的办法舒服些：
u×v=∣∣∣∣iu1v1ju2v2ku3v3∣∣∣∣ $$mathbf{u imes v} = egin{vmatrix} mathbf{i}&mathbf{j}&mathbf{k}\ u_1&u_2&u_3\ v_1&v_2&v_3\ end{vmatrix}$$

要想了解更多，请看维基百科；尽量英文版本，内容丰富准确。

不使用叉积的定义方法

不使用叉积也能轻松表达。当然不是直接代数结果的形式。我说的是使用矩阵。投影矩阵。这个办法实际上在另外一篇博客里面已经使用过。

其几何意义是：
（1）计算直线外的点P$P$与直线上固定点X$X$之间的差值向量；
（2）计算沿直线方向W$W$的初等平行投影矩阵；
（3）把差值向量PX$PX$沿直线方向作投影得到新向量。新向量的模就是点P$P$到直线XW$XW$的距离。

具体的公式此处就不再写了。