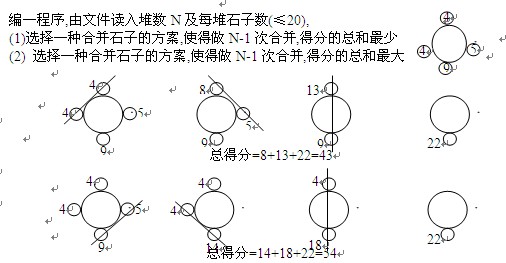
dp泛做1
这里的dp范做根据网上的动态归法分析和网上的有个100个dp方程做的,题解很多是原版,没怎么动,有些是别人的一些其他做法,还有一些自己的想法。如果看到题解很别人一样,那就是摘自别人的。且这里只是一半。
由于本文有些摘自网上,如有原主看到不想在此贴出的,请说明,将会撤出。
如此文方法错误,或者冒犯某些原博主的文章还请见谅,还请指出,非常感谢
机器分配(HNOI’95)
0-1背包变形tyvj1089smrtfun
最长不下降序列(HNOI’97)
石子合并(NOI’95)
凸多边形三角划分(HNOI’97)
乘积最大(noip’2000)
系统可靠性(HNOI’98)
过河(noip’2005)
加分二叉树(noip’2003)
选课(CTSC’98)
砝码称重(noip’96)
核电站问题
数的划分(noip2001)
最大01矩阵
最大子矩阵(Scoi’05)
加+-被k整除(poj1745)
方块消除(poj1390)
装箱问题(noip2001)
数字三角形
晴天小猪历险记同一阶段上暴力动态规划
小胖办证(双向动态规划1,数字三角形)
马拦卒过河noip2002
打砖块(tyvj’1505)
打鼹鼠(CscIIvijos1441)
贪吃的九头龙(NOI2002)
状态压缩dp炮兵阵地(poj1185)
常用递推式子
排列组合中的环形染色问题
隐形的翅膀-线性搜索
陨石的秘密(NOI’2001)
合唱队形(noi2004)
今明的预算方案(noip2006)
花店橱窗布置(IOI’99)
化工厂装箱员
欢乐的聚会spfa+dp
小胖守皇宫(treedp)
活动安排(xtu2012)
有向树k中值问题
CEOI1998 Substract
古城之谜(Noi2000)
单词的划分(tyvj1102)
统计单词个数(Noip2001)
括号序列—tyvj1193
括号序列poj1141
棋盘分割(NOI’99,poj1191)
聪聪和可可(noi2005)
血缘关系
决斗(rqnoj458)
跳舞家怀特先生(tyvj1211)
积木游戏(NOI’97)
逃学的小孩(NOI2003)
机器分配(HNOI’95)
一、问题描述
总公司拥有高效生产设备M台,准备分给下属的N个公司。各分公司若获得这些设备,可以为国家提供一定的盈利。问:如何分配这M台设备才能使国家得到的盈利最大?求出最大盈利值。其中M《=15,N〈=10。分配原则:每个公司有权获得任意数目的设备,但总台数不得超过总设备数M。保存数据的文件名从键盘输入。
数据文件格式为:第一行保存两个数,第一个数是设备台数M,第二个数是分公司数N。接下来是一个M*N的矩阵,表明了第I个公司分配J台机器的盈利。
二、分析
这是一个典型的动态规划试题。用机器数来做状态,数组F[I,J]表示前I个公司分配J台机器的最大盈利。则状态转移方程为
F[I,J]=Max{F[I-1,K] + Value[I,J-K]} (0〈=K〈=J〉
0-1背包变形tyvj1089smrtfun
一、问题描述
现有N个物品,第i个物品有两个属性A_i和B_i。在其中选取若干个物品,使得sum{A_i + B_i}最大,同时sum{A_i},sum{B_i}均非负(sum{}表示求和)。
输入:第一行,一个整数,表示物品个数N。 接下来N行,每行两个整数,表示A_i和B_i。
输出:一个整数,表示最大的sum{A_i + B_i}。
N <= 100 , |A_i| <= 1000 , |B_i| <= 1000
二、分析
首先就是表示状态 f[i]表示当sum{b}为i时sum{a}的最大值,那么sum{b}就相当于背包的体积(可以为负),b[i]就相当于物品的体积(但可以为负值),那没有一个确定的背包体积怎么办呢。。就在线的扩展MAX,初始化MAX=0;比如说第一个b[i];放进去的时候就扩展一下MAX+=b[i];把Ai的和当背包的重量,把Bi的和当成价值来做,每次重量考察Ai和的最小到最大
对于f[]的上限注意了,可不是经典的零。。因为体积(sum{b[i]})可以为负所以就要设置一个MIN来表示其上限。不断地更新MIN,类似MAX那样更新。
最后把j从0到MAX枚举一下
对于当w[i]<0的时候为什么要把for循环那个MIN to MAX+w[i]而不是AX to MIN+w[i];疑问:MIN to MAX+w[i]不就是放无数次,成为完全背包了吗?答:因为w[i]<0.
f[j]:=max(f[j], f[j-a[i]]+b[i])
最长不下降序列(HNOI’97)
一、问题描述
设有整数序列b1,b2,b3,…,bm,若存在i1<i2<i3<…<in,且bi1<bi2<bi3<…<bin,则称 b1,b2,b3,…,bm中有长度为n的不下降序列bi1,bi2,bi3,…,bin。求序列b1,b2,b3,…,bm中所有长度(n)最大不下降子序列
输入:整数序列
输出:最大长度n和所有长度为n的序列个数Total
二、分析
LIS(Longest Increasing Subsequence)最长上升(不下降)子序列,有两种算法复杂度为O(n*logn)和O(n^2)。在上述算法中,若使用朴素的顺序查找在D1..Dlen查找,由于共有O(n)个元素需要计算,每次计算时的复杂度是O(n),则整个算法的时间复杂度为O(n^2),与原来算法相比没有任何进步。但是由于D的特点(2),在D中查找时,可以使用二分查找高效地完成,则整个算法时间复杂度下降为O(nlogn),有了非常显著的提高。需要注意的是,D在算法结束后记录的并不是一个符合题意的最长上升子序列!算法还可以扩展到整个最长子序列系列问题。有两种算法复杂度为O(n*logn)和O(n^2)
O(n^2)算法分析如下
(a[1]...a[n] 存的都是输入的数)
1、对于a[n]来说,由于它是最后一个数,所以当从a[n]开始查找时,只存在长度为1的不下降子序列;
2、若从a[n-1]开始查找,则存在下面的两种可能性:
(1)若a[n-1] < a[n] 则存在长度为2的不下降子序列 a[n-1],a[n].
(2)若a[n-1] > a[n] 则存在长度为1的不下降子序列 a[n-1]或者a[n]。
3、一般若从a[t]开始,此时最长不下降子序列应该是按下列方法求出的:
在a[t+1],a[t+2],...a[n]中,找出一个比a[t]大的且最长的不下降子序列,作为它的后继。
4、为算法上的需要,定义一个数组:
d:array [1..n,1..3] of integer;
d[t,1]表示a[t]
d[t,2]表示从i位置到达n的最长不下降子序列的长度
d[t,3]表示从i位置开始最长不下降子序列的下一个位置
最长不下降子序列的O(n*logn)算法
先回顾经典的O(n^2)的动态规划算法,设A[t]表示序列中的第t个数,F[t]表示从1到t这一段中以t结尾的最长上升子序列的长度,初始时设F[t] = 0(t = 1, 2,..., len(A))。则有动态规划方程:F[t]= max{1, F[j] + 1} (j = 1, 2, ..., t - 1, 且A[j] < A[t])。
现在,我们仔细考虑计算F[t]时的情况。假设有两个元素A[x]和A[y],满足
(1)x < y < t (2)A[x] < A[y] < A[t] (3)F[x] =F[y]
此时,选择F[x]和选择F[y]都可以得到同样的F[t]值,那么,在最长上升子序列的这个位置中,应该选择A[x]还是应该选择A[y]呢?
很明显,选择A[x]比选择A[y]要好。因为由于条件(2),在A[x+1] ... A[t-1]这一段中,如果存在A[z],A[x] < A[z] < a[y],则与选择A[y]相比,将会得到更长的上升子序列。
再根据条件(3),我们会得到一个启示:根据F[]的值进行分类。对于F[]的每一个取值k,我们只需要保留满足F[t] = k的所有A[t]中的最小值。设D[k]记录这个值,即D[k] = min{A[t]} (F[t] = k)。
注意到D[]的两个特点:
(1) D[k]的值是在整个计算过程中是单调不上升的。
(2) D[]的值是有序的,即D[1]< D[2] < D[3] < ... < D[n]。
利用D[],我们可以得到另外一种计算最长上升子序列长度的方法。设当前已经求出的最长上升子序列长度为len。先判断A[t]与D[len]。若A[t] > D[len],则将A[t]接在D[len]后将得到一个更长的上升子序列,len = len + 1, D[len] = A[t];否则,在D[1]..D[len]中,找到最大的j,满足D[j] < A[t]。令k = j + 1,则有D[j] < A[t] <= D[k],将A[t]接在D[j]后将得到一个更长的上升子序列,同时更新D[k] = A[t]。最后,len即为所要求的最长上升子序列的长度。
在上述算法中,若使用朴素的顺序查找在D[1]..D[len]查找,由于共有O(n)个元素需要计算,每次计算时的复杂度是O(n),则整个算法的时间复杂度为O(n^2),与原来的算法相比没有任何进步。但是由于D[]的特点(2),我们在D[]中查找时,可以使用二分查找高效地完成,则整个算法的时间复杂度下降为O(nlogn),有了非常显著的提高。需要注意的是,D[]在算法结束后记录的并不是一个符合题意的最长上升子序列!
这个算法还可以扩展到整个最长子序列系列问题,整个算法的难点在于二分查找的设计,需要非常小心注意。
介绍二:
最长上升子序列LIS算法实现 最长上升子序列问题是各类信息学竞赛中的常见题型,也常常用来做介绍动态规划算法的引例,笔者接下来将会对POJ上出现过的这类题目做一个总结,并介绍解决LIS问题的两个常用算法(n^2)和(nlogn).
问题描述:给出一个序列a1,a2,a3,a4,a5,a6,a7....an,求它的一个子序列(设为s1,s2,...sn),使得这个子序列满足这样的性质,s1<s2<s3<...<sn并且这个子序列的长度最长。输出这个最长的长度。(为了简化该类问题,我们将诸如最长下降子序列及最长不上升子序列等问题都看成同一个问题,其实仔细思考就会发现,这其实只是<符号定义上的问题,并不影响问题的实质)
例如有一个序列:1 7 35 9 4 8,它的最长上升子序列就是 13 4 8 长度为4.
算法1(n^2):我们依次遍历整个序列,每一次求出从第一个数到当前这个数的最长上升子序列,直至遍历到最后一个数字为止,然后再取dp数组里最大的那个即为整个序列的最长上升子序列。我们用dp[i]来存放序列1-i的最长上升子序列的长度,那么dp[i]=max(dp[j])+1,(j∈[1, i-1]); 显然dp[1]=1,我们从i=2开始遍历后面的元素即可。
算法2(nlogn):维护一个一维数组c,并且这个数组是动态扩展的,初始大小为1,c[i]表示最长上升子序列长度是i的所有子串中末尾最小的那个数,根据这个数字,我们可以比较知道,只要当前考察的这个数比c[i]大,那么当前这个数一定能通过c[i]构成一个长度为i+1的上升子序列。当然我们希望在C数组中找一个尽量靠后的数字,这样我们得到的上升子串的长度最长,查找的时候使用二分搜索,这样时间复杂度便下降了。
石子合并(NOI’95)
一、问题描述
在一园形操场四周摆放N堆石子(N≤100),现要将石子有次序地合并成一堆.规定每次只能选相临的两堆合并成一堆,并将新的一堆的石子数,记为该次合并的得分.输入数据:
文件名由键盘输入,该文件内容为:
第一行为石子堆数N;
第二行为每堆石子数,每两个数之间用一空格分隔.
输出数据 :
输出文件名为OUTPUT.TXT
从第1至第N行为得分最小的合并方案. 第N+1行为空行.从N+2到2N+1行是得分最大的合并方案.
每种合并方案用N行表示,其中第i行(1≤i≤N)表示第i次合并前各堆的石子数(依顺时钟次序输出,哪 一堆先输出均可). 要求将待合并的两堆石子数以相应的负数表示,以便识别,参见MODEL2.TXT
参考输入文件EXAMPLE2.TXT
4
4 5 9 4
参考输出文件MODEL2.TXT
-4 5 9 -4
-8 -5 9
-9 -13
-22
4 -5 -9 4
4 -14 -4
-4 –18
-22
二、分析
看到本题,容易想到使用贪心法,即每次选取相邻最大或最小的两堆石子合并。
然而这样做对不对呢?看一个例子。
N=5 石子数分别为3 4 6 5 4 2。
用贪心法的合并过程如下:
第一次 3 4 65 4 2得分 5
第二次 5 4 65 4得分9
第三次 9 6 5 4得分9
第四次 9 6 9得分15
第五次 15 9得分24
第六次24
总分:62
然而仔细琢磨后,发现更好的方案:
第一次3 4 65 4 2得分 7
第二次7 6 54 2得分13
第三次13 5 4 2得分6
第四次13 5 6得分11
第五次 13 11得分24
第六次24
总分:61
显然,贪心法是错误的。
为什么?
显然,贪心只能导致局部的最优,而局部最优并不导致全局最优。
仔细分析后,我们发现此题可用动态规划进行解决。
我们用data[I,j]表示将从第i颗石子开始的接下来j颗石子合并所得的分值,
max[i,j]表示将从第i颗石子开始的接下来j颗石子合并可能的最大值,那么:
max[I,j] = max(max[i, k] + max[i + k, j – k] + data[I,k] + data[I + k, j – k]) (2<=k<=j)
max[i,1] = 0
同样的,我们用min[i,j]表示将第从第i颗石子开始的接下来j颗石子合并所得的最小值,可以得到类似的方程:
min[I,j] = min(min[i, k] + min[i + k, j – k] + data[I,k] + data[I + k, j – k]) (0<=k<=j)
min[I,0] = 0
这样,我们完美地解决了这道题。空间复杂度为O(n2),时间复杂度也是O(n2)。
动态规划思路:
阶段i:石子的每一次合并过程,先两两合并,再三三合并,...最后N堆合并
状态s:每一阶段中各个不同合并方法的石子合并总得分。
决策:把当前阶段的合并方法细分成前一阶段已计算出的方法,选择其中的最优方案
具体来说我们应该定义一个数组s[i,j]用来表示合并方法,i表示从编号为i的石头开始合并,j表示从i开始数j堆进行合并,s[i,j]为合并的最优得分。
对于上面的例子来说,初始阶段就是s[1,1],s[2,1],s[3,1],s[4,1],s[5,1],s[6,1],因为一开始还没有合并,所以这些值应该全部为0。
第二阶段:两两合并过程如下,其中sum(i,j)表示从i开始数j个数的和
s[1,2]=s[1,1]+s[2,1]+sum(1,2)
s[2,2]=s[2,1]+s[3,1]+sum(2,2)
s[3,2]=s[3,1]+s[4,1]+sum(3,2)
s[4,2]=s[4,1]+s[5,1]+sum(4,2)
s[5,2]=s[5,1]+s[6,1]+sum(5,2)
s[6,2]=s[6,1]+s[1,1]+sum(6,2)
第三阶段:三三合并可以拆成两两合并,拆分方法有两种,前两个为一组或后两个为一组
s[1,3]=s[1,2]+s[3,1]+sum(1,3)或s[1,3]=s[1,1]+s[2,2]+sum(1,3),取其最优
s[2,3]=s[2,2]+s[4,1]+sum(2,3)或s[1,3]=s[2,1]+s[3,2]+sum(2,3),取其最优
...
第四阶段:四四合并的拆分方法用三种,同理求出三种分法的得分,取其最优即可。以后第五阶段、第六阶段依次类推,最后在第六阶段中找出最优答案即可
凸多边形三角划分(HNOI’97)
一、试题描述
给定一个具有N(N<50)个顶点(从1到N编号)的凸多边形,每个顶点的权均已知。问如何把这个凸多边形划分成N-2个互不相交的三角形,使得这些三角形顶点的权的乘积之和最小?
输入文件:第一行 顶点数N
第二行 N个顶点(从1到N)的权值
输出格式:最小的和的值
各三角形组成的方式
输入示例:5
121 122 123 245 231
输出示例:The minimum is :12214884
The formation of 3 triangle:
3 4 5, 15 3, 1 2 3
二、试题分析
这是一道很典型的动态规划问题。设F[I,J](I<J)表示从顶点I到顶点J的凸多边形三角剖分后所得到的最大乘积,我们可以得到下面的动态转移方程:
F[I,J]=Min{F[I,K]+F[K,J]+S[I]*S[J]*S[K]} (I<K<J)
目标状态为:F[1,N]
但我们可以发现,由于这里为乘积之和,在输入数据较大时有可能超过长整形甚至实形的范围,所以我们还需用高精度计算,但这是大家的基本功,程序中就没有写了,请读者自行完成。
乘积最大(noip’2000)
问题描述:
一道题目:设有一个长度N的数字串,要求选手使用K个乘号将它分成K+1个部分,找出一种分法,使得这K+1个部分的乘积能够为最大。同时,为了帮助选手能够正确理解题意,主持人还举了如下的一个例子:
有一个数字串: 312,当N=3,K=1时会有以下两种分法:
1)3*12=36
2)31*2=62
这时,符合题目要求的结果是: 31*2=62
输入:程序的输入共有两行:
第一行共有2个自然数N,K(6<=n<=40,1<=k<=6)
第二行是一个K度为N的数字串。
输出:结果显示在屏幕上,相对于输入,应输出所求得的最大乘积(一个自然数)。
输入
4 2
1231
输出
62
分析:
设字符串长度为n,乘号数为k,如果n=50,k=1时,有(n-1)=49种不同的乘法,当k=2时,有C(2,50-1)=1176种乘法,既C(k,n-1)种乘法,当n、k稍微大一些的时候,用穷举的方法就不行了。
设数字字符串为a1a2…an
K=1 时:一个乘号可以插在a1a2…an中的n-1个位置,这样就得到n-1个子串的乘积:
a1*a2…an, a1a2*a3…an, …, a1a2…a n-1*an( 这相当于是穷举的方法)
此时的最大值= max{a1*a2…an,a1a2*a3…an, …, a1a2…a n-1*an }
K=2时,二个乘号可以插在a1a2…an中n-1个位置的任两个地方, 把这些乘积分个类,便于观察规律:
①最后一个数作为被乘数:
a1a2 …*a n-1*an , a1a2 …*a n-2 a n-1*an , a1*a2 …a n-3 a n-2 a n-1*an
设符号F[n-1,1]为在前n-1个数中插入一个乘号的最大值,则的最大值为F[n-1,1]*an
②最后2个数作为被乘数:
a1a2 …*a n-2*a n-1an , a1a2 …*a n-3 a n-2* an-1 an , a1*a2 …an-3 a n-2*an-1an
设符号F[n-2,1]为在前n-2个数中插入一个乘号的最大值,则的最大值为F[n-2,1]*an-1an
③最后3个数作为被乘数:
设符号F[n-3,1]为在前n-3个数中插入一个乘号的最大值,则最大值为F[n-3,1]+an-2an-an
……
a3~an作为被乘数:F[2,1]*a3 …an-2an-1an
此时的最大乘积为:
F[n,k]=max{F[n-1]*an,F[n-2,1]*an-1an,F[n-3,1]*an-2an-1an,F[2,1]*a3…an-2an-1an}
设F[i,j]表示在 i 个数中插入 j 个乘号的最大值,g[i,j]表示从ai到aj的数字列,则可得到动规方程:
F[I,j]= max{F[I-1,j-1]*g[I,I],F[I-2,j-1]*g[I-1,I],F[I-3,j-1]*g[I-2,I],
…,F[j,j-1]*g[j+1,I]}(1<=I<=n, 1<=j<=k)
边界: F[I,0] =g[1,I] (数列本身)
阶段:子问题是在子串中插入j-1,j-2……1,0个乘号,因此乘号个数作为阶段的划分(j个阶段)
状态:每个阶段随着被乘数数列的变化划分状态。
决策:在每个阶段的每种状态中做出决策。
还有2个问题需要注意:
(1)输入的字符需要进行数值转换
(2)由于乘积可能很大,所以可以使用大数类型
参考程序
系统可靠性(HNOI’98)
一、问题描述:
给定一些系统备用件的单价Ck,以及当用Mk个此备用件时部件的正常工作概率Pk(Mk),总费用上限C。求系统可能的最高可靠性。
输入:第一行:n C
第二行:C1 P1(0) P1(1) … P1(X1) (0<=X1<=[C/Ck])
…
第 n 行:Cn Pn(0) Pn(1) … Pn(Xn) (0<=Xn<=[C/Cn])
输出:最大可靠性的值
样例
输入:
2 20
3 0.6 0.65 0.7 0.75 0.8 0.85 0.9
5 0.7 0.75 0.8 0.8 0.9
输出:0.6375
二、算法分析
1.证明这个问题符合最优化原理。可以用反证法证明之。假设用money的资金购买了前I项备用件,得到了最高的系统可靠性,而且又存在如下情况:对于备用件I,设要买Ki个,则可用的资金还剩余money– Ci*Ki,用这些钱购买前(I-1)项备用件,如果存在一种前(I-1)种备用件的购买方案得到的系统可靠性比当前得到的要高,那么这个新的方案会使得整个前I项备用件组成的系统可靠性比原先的更高,与原假设矛盾。所以可以证明这个问题符合最优化原理。
2.证明这个问题符合无后效性原则。
3.综上所述,本题适合于用动态规划求解。
4.递推方程及边界条件:
F[I,money] :=max { F[I-1,money – C[I]*K[I] ] } (0<=K[I]<=C div Ci )
三、参考程序
过河(noip’2005)
一、 问题描述
在河上有一座独木桥,一只青蛙想沿着独木桥从河的一侧跳到另一侧。在桥上有一些石子,青蛙很讨厌踩在这些石子上。由于桥的长度和青蛙一次跳过的距离都是正整数,我们可以把独木桥上青蛙可能到达的点看成数轴上的一串整点:0,1,……,L(其中L是桥的长度)。坐标为0的点表示桥的起点,坐标为L的点表示桥的终点。青蛙从桥的起点开始,不停的向终点方向跳跃。一次跳跃的距离是S到T之间的任意正整数(包括S,T)。当青蛙跳到或跳过坐标为L的点时,就算青蛙已经跳出了独木桥。
题目给出独木桥的长度L,青蛙跳跃的距离范围S,T,桥上石子的位置。你的任务是确定青蛙要想过河,最少需要踩到的石子数。
对于30%的数据,L <= 10000;
对于全部的数据,L <= 10^9。
输入:第一行有一个正整数L(1 <= L <= 10^9),表示独木桥的长度。第二行有三个正整数S,T,M,分别表示青蛙一次跳跃的最小距离,最大距离,及桥上石子的个数,其中1 <= S <= T <= 10,1 <= M <= 100。第三行有M个不同的正整数分别表示这M个石子在数轴上的位置(数据保证桥的起点和终点处没有石子)。所有相邻的整数之间用一个空格隔开
输出:输出只包括一个整数,表示青蛙过河最少需要踩到的石子数。
样例:10
2 3 5
2 3 56 7
输出:2
分析:
1.分s=t和s<t考虑。当s=t时,只需要考虑第i个位置上有石子且i mod s=0的情况;
2.当s<t时,压缩桥长和石子位置(要考虑到石子位置不一定有序),若两石子间空白区>maxk+2*t,我们就把它缩短为前一个石子位置加上maxk+2*t(可证得maxk=100时满足所有区间);
3.从1到L(压缩后最后一个石子位置)+t-1进行动态规划,f[i]=min{f[i-j]+1(如果i处不为石子),f[i-j](如果i处为石子)}(j=s..t,f[i]初始值为100,最多有100颗石子);
4.答案就是min{f[L],f[L+1],...,f[L+t-1]}。
这题因为 1 <= L <= 10^9 L非常大,只能进行状态压缩。如果 L小到可以开数组,我们可以设一个数组Dp[L_MAX]保存每个子状态,从后往前DP,Dp[n] 表示从坐标位置 n 跳到或者跳过终点的最优解(局部最优),求Dp[n-1],Dp[n-1] = min{Dp(n-1+minJump ~ n-1+maxJump)},minJump表示青蛙最小的跳数,maxJump表示青蛙最大的跳数,如果 n-1 位置有石头则Dp[n-1]=Dp[n-1]+1.
比如对于示例:
10
2 3 5
2 3 56 7
首先我们初始化数组,Dp[]={0},从坐标位置7开始算,Dp[7]=min{Dp(2+7,3+7)}=0,因为7位置有石头所以Dp[7]=Dp[7]+1=1,同理,Dp[6]=1,Dp[5]=1,Dp[4] = min{Dp(4+2,4+3)} = 1,因为5位置没有石头所以Dp[4]不用加1,最后可求得 Dp[] = {2,1,2,2,1,1,1,1,0,0,0 ……},Dp[0]即为全局的最优解,表示从起点跳到或者跳过终点青蛙最少要踩到的石头数目。
这题因为L很大,子状态不能全部保存,我们观察到,当求Dp[n]的值时用到的状态只有
Dp(n+minJump,n+maxJump)所以我们可以不用全部保存每个坐标位置的Dp值,而只要保存从n位置之后最多maxJump个坐标的Dp值即可。为此我们可设Dp[maxJump](对本题可设Dp[10]),注意这里的下标不表示坐标位置,我们可用一个变量nHeadStart跟踪坐标位置,当求n位置的Dp值时,nHeadStart=n+1。到这里我们解决了空间问题,真正难理解的是下面的状态压缩。
假如测试数据是:
1000000000
2 5 5
2 6 510 99999999
99999999这个位置的Dp值我们知道是 1,而该位置前面有99999999-10个位置都没有石头,我们不可能也没有时间去求所有这些中间位置的Dp值,但是10位置的值却与这中间的有关,HowCan I do ???假如有这样一组Dp值,Dp[]={25 1 3} 我们观察到单minJump != maxJump时,因为每次都取最小值所以经过有限步运算后,Dp={1 1 1 1},即所有的Dp值都变成开始计算时的最小值。变化经过如下
数据:minJump=2, maxJump=3,Dp[]={2,5,1,3}
Dp[]={1,2,5,1}
Dp[]={1,2,2,5}
Dp[]={2,1,2,2}
Dp[]={1,2,1,2}
Dp[]={1,1,2,1}
Dp[]={1,1,1,2}
Dp[]={1,1,1,1}
即从当前位置到前面 7 个及 7 个以前的空位(没有石头),我们断定Dp[]={1,1,1,1}
因此,对 2 6 5 10 99999999,我们可以知道从 11 位置开始,Dp[]={0,0,0,0,0}(只需保存maxJump个)前面的就好做了。经过几步的空位可以达到稳定状态(我称Dp数组值不再变化的状态为稳定态),我们有两种方法
其一:每求一个空位后我们求Dp数组中的最值,如果最大和最小值相等就达到稳定态了。这种方 法因为每次都要求最值,因此当maxJump比较大的时候不适合。
其二:我们可以断定如果当前位置之前至少有maxJump*maxJump个空位,就一定会出现稳定态(请读者自己理解 这样我们遇到空位大于等于maxJump*maxJump时直接设Dp数组为最小值。
上面的是minJump != maxJump的情况,当minJump==maxJump时,假如Dp[]={0,0,1}
数据:minJump=3, maxJump=3,Dp[]={0,0,1},Dp的变化情况如下:
Dp[]={1,0,0}
Dp[]={0,1,0}
Dp[]={0,0,1}
......
出现重复的情况,且min{Dp[]} != max{Dp[]},因此不能按minJump !=maxJump的情况处理。这种情况只要将重复出现的位去掉即可,比如上面的如果当前位置前有 4 个空位,前三个不用计算,因为到第三个位置的Dp值和当前的Dp值一样。
Dp[]数组的下标变化大家可以参考循环队列的情况。
关于压缩空长条步数的证明
对于步幅s到t 若目标位置距起始点距离D≥s×(s+1)则一定可以到达目标点
证明:
设一次可以走p步或p+1 方便起见,我们取起始位置为坐标0点
那么p×(p-1)点一定可以达到(每次走p的距离,走p-1次)
因为我们也可以每次走p+1步
所以可以通过将一次p距离的行走替换为p+1距离的行走来实现总距离+1
比如说我们要达到p×(p-1)+1点我们只需要走p-2次p的距离和一次p+1的距离即可到达
我们整理两个表达式p×(p-1)+1和(p-2)×p+(p+1)就可证明上述正确
现在我们从(p-1)×p位置开始逐一推算可行性
(p-1)×p+1=(p-2)×p+(p+1)
(p-1)×p+2=(p-3)×p+(p+1)×2
(p-1)×p+3=(p-4)×p+(p+1)×3
……
(p-1)×p+(p-1)=(p-p)×p+(p+1)(p-1)
我们已经用光了所有可以替换的p距离行走。
那么(p-1)×p+p如何实现呢?
对上面多项式整理得:p×p
显然我们只需要进行p次p距离的行走就可以到达目标
也就是说我们通过用p+1代换p的方法前进p-1步
在前进第p步时重新整合成关于p的多项式(一定是p的倍数)如此往复。
而我们要前进p-1步至少需要p-1个p。所以下限为p×(p-1)
至此,命题得证。
加分二叉树(noip’2003)
一、问题描述
设一个n个节点的二叉树tree的中序遍历为(l,2,3,…,n),其中数字1,2,3,…,n为节点编号。每个节点都有一个分数(均为正整数),记第j个节点的分数为di,tree及它的每个子树都有一个加分,任一棵子树subtree(也包含tree本身)的加分计算方法如下:
subtree的左子树的加分× subtree的右子树的加分+subtree的根的分数
若某个子树为主,规定其加分为1,叶子的加分就是叶节点本身的分数。不考虑它的空子树。
试求一棵符合中序遍历为(1,2,3,…,n)且加分最高的二叉树tree。要求输出;
1)tree的最高加分
2)tree的前序遍历
输入格式 InputFormat
第1行:一个整数n(n<30),为节点个数。
第2行:n个用空格隔开的整数,为每个节点的分数(分数<100)。
输出格式 OutputFormat
第1行:一个整数,为最高加分(结果不会超过4,000,000,000)。
第2行:n个用空格隔开的整数,为该树的前序遍历。
样例输入:5
5 7 1 2 10
样例输出:5
5 7 1 2 10
二、分析:
区间DP。
用f[i,j]表示合并[i,j]这段区间的最大加分,k为根,则有
f[i,j]:=max(f[i,k]*f[k,j]+score[k]);{i<=k<=j}
边界是空树的加分为1,单位区间的最大加分为本身的加分。
目标为f[1,n];
由于要输出方案,所以在转移时记录转移的k.最后递归输出即可。
注意就是先循环长度,再枚举开始位置,用长度和开始位置求出结束位置之后再枚举k。因为转移的时候,要求比当前区间短的区间都要知道。
------------------
先画画这种树算算样例
发现每个树划分为左右子数后 左右子树也是按照同样的方法划分 形成了重叠子结构
马上想到区间DP 配合四边形不等式O(N*N)
选课(CTSC’98)
一、问题描述
大学里实行学分。每门课程都有一定的学分,学生只要选修了这门课并考核通过就能获得相应的学分。学生最后的学分是他选修的各门课的学分的总和。
每个学生都要选择规定数量的课程。其中有些课程可以直接选修,有些课程需要一定的基础知识,必须在选了其它的一些课程的基础上才能选修。例如,《数据结构》必须在选修了《高级语言程序设计》之后才能选修。我们称《高级语言程序设计》是《数据结构》的先修课。每门课的直接先修课最多只有一门。两门课也可能存在相同的先修课。为便于表述每门课都有一个课号,课号依次为1,2,3,……。下面举例说明
|
课号 |
先修课号 |
学分 |
|
1 |
无 |
1 |
|
2 |
1 |
1 |
|
3 |
2 |
3 |
|
4 |
无 |
3 |
|
5 |
2 |
4 |
上例中1是2的先修课,即如果要选修2,则1必定已被选过。同样,如果要选修3,那么1和2都一定已被选修过。
学生不可能学完大学所开设的所有课程,因此必须在入学时选定自己要学的课程。每个学生可选课程的总数是给定的。现在请你找出一种选课方案,使得你能得到学分最多,并且必须满足先修课优先的原则。假定课程之间不存在时间上的冲突。
输入
输入文件的第一行包括两个正整数M、N(中间用一个空格隔开)其中M表示待选课程总数(1≤M≤1000),N表示学生可以选的课程总数(1≤N≤M)。
以下M行每行代表一门课,课号依次为1,2……M。每行有两个数(用一个空格隔开),第一个数为这门课的先修课的课号(若不存在先修课则该项为0),第二个数为这门课的学分。学分是不超过10的正整数。
输出
输出文件第一行只有一个数,即实际所选课程的学分总数。以下N行每行有一个数,表示学生所选课程的课号。
二、分析
本题看上去不太好动手。这是一道求最优解的问题,如果用搜索解题,那规模未免过于庞大;用动态规划,本题数据之间的关系是树形,和我们往常见到线性的数据关系不一样。
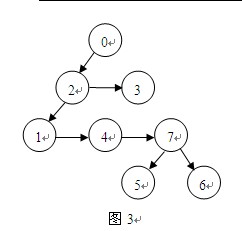
怎么办?我们先从一些简单的数据入手分析。如表1所示的输入数据,我们可将它看为由两棵树组成的森林,如图1所示。
我们添加一个顶点0,并且在每棵树的顶点与0之间连一条边使森林成为一棵树,如图2。
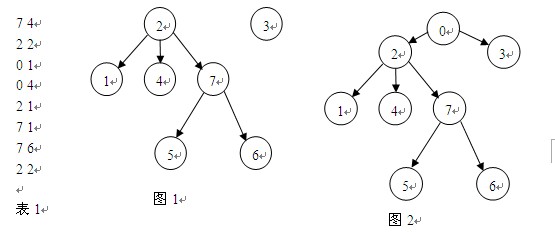
我们发现,我们可以选取某一个点k的条件只是它的父节点已经被选取或者它自己为根节点;而且我们不论如何取k的子孙节点,都不会影响到它父节点的选取情况,这满足无后效性原则。于是我们猜测,是不是可以以节点为阶段,进行动态规划呢?
我们用函数f(I,j)表示以第i个节点为父节点,取j个子节点的最佳代价,则:
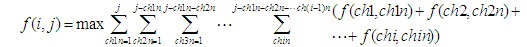
可是如此规划,其效率与搜索毫无差别,虽然我们可以再次用动态规划来使它的复杂度变为平方级,但显得过于麻烦。
我们继续将树改造:原本是多叉树,我们将它转变为二叉树。如果两节点a,b同为兄弟,则将b设为a的右节点;如果节点b是节点a的儿子,则将节点b设为节点a的左节点。树改造完成后如图3。
我们用函数f(I,j)表示以第i个节点为父节点,取j个子节点的最佳代价,这和前一个函数表示的意义是一致的,但方程有了很大的改变:

这个方程的时间复杂度最大为n3,算十分优秀了。
在具体实现这道题时,我们可以自顶而下,用递归进行树的遍历求解;在空间方面,必须特别注意。因为如果保存每一个f(I,j),bp下是不可能的。我们必须用多少开多少,这样刚好可以过关。(具体请参见程序)
分析(自)
很容易想到在树上背包来解决问题,假设f[i][j]为以i为根的子树,包括i,选择j门课的最大值
那么有f[i][j]=max{ f[i][a]+f[k][b] }k是i的子树,a+b=j
这样的复杂度是O(n*m^2)对于这题的数据范围来说还是够用的,不过我用上了对这种泛化物品的背包的一种优化复杂度降为O(n*m)
砝码称重(noip’96)
一、 问题描述
设有1g、2g、3g、5g、10g、20g的砝码各若干枚(其总重<=1000),用他们能称出的重量的种类数。
输入:a1 a2 a3 a4 a5 a6表示1g砝码有a1个,2g砝码有a2个,…,20g砝码有a6个,中间有空格)。
输出:Total=N(N表示用这些砝码能称出的不同重量的个数,但不包括一个砝码也不用的情况)。
样例输入 1 1 0 0 0 0
样例输出 3
二、分析
就是个01背包……f[0]:=true把问题稍做一个改动,已知a1+a2+a3+a4+a5+a6个砝码的重量w[i], w[i]∈{ 1,2,3,5,10,20} 其中砝码重量可以相等,求用这些砝码可称出的不同重量的个数。这样一改就是经典的0/1背包问题的简化版了,求解方法完全和上面说的一样
设dp[1000]数组为标记数组。当dp[i]=0时,表示质量为i的情况,目前没有称出;当dp[i]=1时,表示质量为i的情况已经称出。题目中有多个砝码,我们顺序处理每一个砝码。当处理第j个砝码,质量为wj时,有下列推导公式:
d[i-wj]=1==>d[i]=1(当且仅当质量i-wj已经称出,才能称出质量i)
核电站问题
一、题目描述
一个核电站有N个放核物质的坑,坑排列在一条直线上。如果连续M个坑中放入核物质,则会发生爆炸,于是,在某些坑中可能不放核物质。
现在,请你计算:对于给定的N和M,求不发生爆炸的放置核物质的方案总数。
二、分析
法1:设f[i]为第i个位置不爆炸的方案数,注意!这个f一定是合法的!则这个位置可以放/不放,(别急,不一定合法~)f[i-1]*2但不能连续放m个,所以>=m时需要减去保证只连了m个,即前m-1全放了,而i-m(绿圈)一定不放 的 1种情况
----f[i-m-1]<---(合法的) 不管它是如何组成的,这是dp的精髓正对的头是i-m+1
而初始值f[0]=1有意义,第0个就是不放。但f[-1]是由 推f[m]=f[m-1]*2-f[i(m)-m-1]为了正解,设的f[-1]=1
数的划分(noip2001)
一、问题描述
将整数n分成k份,且每份不能为空,任意两份不能相同(不考虑顺序)。
例如:n=7,k=3,下面三种分法被认为是相同的。
1,1,5; 1,5,1; 5,1,1;
问有多少种不同的分法。
输入:n,k(6<n<=200,2<=k<=6)
输出不同分法
例如:7 3 输出4
分析:用f(I,j)表示将整数I分成j分的分法,可以划分为两类:
第一类 :j分中不包含1的分法,为保证每份都>=2,可以先那出j个1分到每一份,然后再把剩下的I-j分成j份即可,分法有:f(I-j,j).
第二类 : j份中至少有一份为1的分法,可以先那出一个1作为单独的1份,剩下的I-1再分成j-1份即可,分法有:f(I-1,j-1).
所以:f(I,j)=f(I-j,j)+ f(I-1,j-1)
最大01矩阵
一、题目描述
给定一个n*m的01矩阵
如果在一个矩形中,边框上的数都是1,其余数都是0,那么我们称这个矩形为0类矩形
形如
11111
10001
11111
答案:15
Your Task:求出面积最大的0类矩形的面积s
输入:第一行两个数n、m。接下来n行每行m个数。n <= 2000,m <= 2000
输出:每行一个数s
二、分析
本题中符合要求的矩形可以分为2种:
1.1*k和2*k
2.k1 * k2的
对于第一种,由于这种矩形全部是由1构成的,扫描一次更新答案就可以了。
对于第二种,注意到里面那层0构成0的一个极大联通块。因此,我们只用找出每一个0的极大联通块,然后判断是否是题目要求的图形就可以了。
在判断的时候,只用注意3个地方:
1.是否有0延伸到了矩阵的边缘,有的话显然不符合要求
2.这个联通块是否构成一个矩形。构不成矩形显然也不行。
3.周围的1是否能构成一个完整的壳。
具体实现的时候,可以记录这个极大联通块所能延伸到最远的行列。即程序中的max_row,min_row,max_column,min_column。以及当前块的面积sum.
然后对1,只用判断是这四个值是否等于对应的边界。
对于2,只用判断又这四个行列所确定的矩形面积是否等于sum。
对于3,只用判断加上1之后的大矩形四个角是为1,因为边是一定全部为1的。
这样,就可以在O(mn)的时间内解决本题了。
最大子矩阵(Scoi’05)
一、问题描述
这里有一个n*m的矩阵,请你选出其中k个子矩阵,使得这个k个子矩阵分值之和
最大。注意:选出的k个子矩阵不能相互重叠。
输入格式:第一行为n,m,k(1≤n≤100,1≤m≤2,1≤k≤10),接下来n行描述矩阵每行中的每个元素的分值(每个元素的分值的绝对值不超过32767)。
输出格式:只有一行为k个子矩阵分值之和最大为多少
样例输入:
3 2 2
1 -3
2 3
-2 3
输出:9
二、分析
由于m<=2可以分情况讨论
(1)m = 1 时就相当于1维,用g[i][j]表示前i个数字选出j段的最大分值转移是O(N)的,往前枚举即可
(2)m = 2时f[i][j][k]表示第一列前i个数字,第二列前j个数字选出k个子矩阵的最大分值转移还是O(N)
f[i][j][k] =max(f[i - 1][j][k], f[i][j - 1][k]);
f[i][j][k] =max{ f[i][j][k], f[x][j][k - 1] + s1[i] - s1[x] };
f[i][j][k] =max{ f[i][j][k], f[i][y][k - 1] + s2[j] - s2[y] };
当 i = j 时 f[i][j][k] = max{ f[i][j][k], f[x][x][k - 1] + s1[i] - s1[x] +s2[i] - s2[x] }
如果是 2*n 的话用 a1 表示第一行的个数,a2表示第二行,k表示选出矩阵个数DP情况是靠最后一个矩阵是否在边界上。如果a1 != a2 那么dp(k,a1,a2) = max(dp(k,a1-1,a2),dp(k,a1,a2-1),dp(k-1,a1-j,a2)+ value(第k矩阵),dp(k-1,a1,a2-j) +value(第k矩阵)),a1 == a2,那么就有可能是最后一个矩阵是一个2*j的矩阵。那么就还有可能最大的是这种情况那么就加dp(k,a1,a2) = max(dp(k,a1,a2),dp(k-1,a1-j,a2-j) + value(第k矩阵))
加+-被k整除(poj1745)
一、题目描述:n个整数中间填上+或者-,运算结果能否被k整除。1<=n<=10000,2<=k<=100
二、分析:已知(a+b)%m =(a%m + b%m)%m;那么f[i,j] 表示 前i个数运算结果mod k是否存在余数j,转移方程就简单了:如果f( i-1, j)为true,那么把f(i,(j+a[i])mod k)和f(i, (j-a[i])mod k)置真。由于可能会出现复数的情况,处理可以要么把数组开到负的,要么加一个很大的k的倍数再mod。要么特判
方块消除(poj1390)
一、问题描述:一款叫做方块消除的游戏。游戏规则如下:n个带颜色方格排成一列,相同颜色的方块连成一个区域(如果两个相邻方块颜色相同,则这两个方块属于同一区域。游戏时,你可以任选一个区域消去。设这个区域包含的方块数为x,则将得到x^2个分值。方块消去之后,其余的方块就会竖直落到底部或其他方块上。而且当有一列方块被完全消去时,其右边的所有方块就会向左移一格。虽然游戏很简单,但是要拿高分也很不容易。找出得最高分的最佳方案
输入格式:第一行包含一个整数n(0<=n<=100),表示方块数目。第二行包含n个数,表示每个方块的颜色(1到n之间的整数)。
输出格式:仅一个整数,即最高可能得分。
二、分析
/*设计状态f[i,j,k]表示[i..j]段序列和后面的k个方块消去所得到的最大值。说明:
后面的k个方块是火星来的咩?肯定不是...是后面的某个区间有k个方块,暂且称之为late。此区间的颜色和j区间相同。消掉了j和late区间中间的方块,于是j区间和late区间就连在一起了,并且消掉[j+1..late-1]的这一块的值是在上一步子问题中解决的,在这一个子问题中体现不出来。
刚开始看别人的解释也是一头雾水,后来看了程序就明白了。
子问题是一段区间的序列怎么消,和别人一起消,还是自己消了算了。
len[late]=k;colour[j]=colour[late];现在late和j紧挨在一起,可以算是一个区间了。
状态转移:
f[i,j,k]:=f[i,j-1,0]+(len[j]+k)^2;如果现在就将j和late的和区间消掉。
f[i,j,k]:=f[i,p,len[j]+k]+f[p+1,j-1,0];(colour[p]=colour[j]=colour[late])如果j和late再和前面的某一区间合并后再消掉。从这里也可以看出为什么求解f[i,p,len[j]+k]这一个子问题的时候没有求到f[p+1,j-1,0]这一部分,这解释了上一部分中的斜体字部分。
f[i,j,k]:=(len[i]+k)*(len[i]+k);(i=j);
用f [ i ] [ j ] [ k] 表示把(color [ i ] , len [ i ] ), (color [ i+1 ] , len [ i+1 ] ) ,……, (color [j-1 ] , len [ j-1 ] ),(color [j ] , len [ j ]+k )合并的最大得分
考虑(color [ j ] ,len [ j ]+k )这一段要不马上消去 要不和前面的一起消去
如果马上消去:f【i】【j-1】【0】+(len【j】+k)^2
如果和前面一起消去 那么前面有的段数可以有P位 那么得分可以有P种情况
f【i】【p】【k+len[j]】+f【p+1】【j-1】【0】;(color【p】=color【j】 i<=p<j)
所以f 【i】【j】【k】=两个的最大值. 边界条件是f【i】【i-1】【0】=0*/
装箱问题(noip2001)
一、问题描述:有一个箱子容量为V(正整数,0<=V<=20000),同时有n个物品(0<n<=30=,每个物品有一个体积(正整数)。要求n个物品中,任取若干个装入箱内,使箱子的剩余空间为最小。
二、分析:首先,对于第I个背包,有选与不选两种状态。我们设F[i]表示使用容量为i的背包所获得的最大价值,则F[i]:=Max(F[i-w[i]]+a[i],F[i])这个状态转移方程
数字三角形
示出了一个数字三角形。 请编一个程序计算从顶至底的某处的一条路径,使该路径所经过的数字的总和最大。每一步可沿左斜线向下或右斜线向下走;1<三角形行数<25;
三角形中的数字为整数<1000;
晴天小猪历险记同一阶段上暴力动态规划
一、问题描述:晴天小猪来到了一座深山的山脚下,因为只有这座深山中的一位隐者才知道这种药草的所在。但是上山的路错综复杂,由于小小猪的病情,晴天小猪想找一条需时最少的路到达山顶,山用一个三角形表示,从山顶依次向下有1段、2段、3段等山路,每一段用一个数字T(1<=T<=100)表示,代表晴天小猪在这一段山路上需要爬的时间,每一次它都可以朝左、右、左上、右上四个方向走(注意:在任意一层的第一段也可以走到本层的最后一段或上一层的最后一段)。晴天小猪从山的左下角出发,目的地为山顶,即隐者的小屋。
输入格式:第一行有一个数n(2<=n<=1000),表示山的高度。从第二行至第n+1行,第i+1行有i个数,每个数表示晴天小猪在这一段山路上需要爬的时间。
输出格式:一个数,即晴天小猪所需要的最短时间。
输入
5
1
2 3
4 5 6
10 1 7 8
1 1 4 5 6
输出:10
二、分析
DP数字三角形的一个扩展,一道好题。可得dp方程
f[i,j]=min{f[i-1,j-1],f[i-1,j],f[i,j-1],f[i,j+1]}+a[i,j]
边缘的走法:
(5, 1)能走到(5, 5)(5, 2)(4, 1)(4, 4)
(5, 5)能走到(5, 1)(5, 4)(4, 1)(4, 4)
重诉一下题目的意思,第一小猪走的方向有四个左上,右上,左,右,在任意一层的第一段也可以走到本层的最后一段或上一层的最后一段,而最后一段也可以走到第一段。找从左下角走到山顶的最少时间。第二数据给出的是圆锥形的。
1
2 3
4 5 6
9 1 7 8
1 1 4 5 6
与数字三角形不同的地方就是可以左,右走,在任意一层的第一段也可以走到本层的最后一段或上一层的最后一段,而最后一段也可以走到第一段。第一段和最后一段的特殊性可以单独判断,重点在于如何去掉左右走的后效性,和找出当前的最小值。这里说一种简单的方法,网上大多数的人都用这种方法也做这道题。就是先进 行左上和右上的操作这样就一定有一个已经确定了的最小值,它在左,右操作都不会被改变,因为下面一层已经计算出最优值,它一定是由那下面直接走上来的。然后由这个点去改变其他点,然后判断出第一个和最后一个的值,是否可以再次被改变。再从头到尾循环一次,从尾到头循环一次,这样就可以计算出当前一层的最优 值,这样一值做到第一层。
网上的题解:
1.DP有环怎么办?
别急,先别想着放弃DP,有时候环是可以避免的.这里在每一行中为避免相邻两格左右移动产生的环,可以先推向左的,再推向右的,而同向移动产生的那个“大”环就麻烦一点.其实有个很简单的窍门:先记录从下一行转移来的最优值,然后在本行中寻找代价最小的点,以这个点为起点分别向左向右推,因为最小的点 显然是不需要从两侧的点过来的.这样就没有后效性了..
2.递推的顺序:
递推有两种顺序,可以根据当前状态值推出所有可能的后继状态,也可以根据所有当前状态可能的前驱来推当前值,很多时候,当问题的状态比较有规律时,这两种 方法是不相上下的.但是其他情况下一不小心就可能搞错.比如这题题目告诉我们的是从一个状态可行的所有走法(共四种),所以根据这个顺序去编是最保险的。 因为这里一个状态的前驱不一定只是四个,边缘的点是特例,可能会有5个来源,所以DP的时候不要随便换状态转移顺序.
这道题还可以用最短路经算法来做,把两个可以走的点看成一条边。
对于程序,可以自己画个图
小胖办证(双向动态规划1,数字三角形)
问题描述:xuzhenyi要办个签证。办证处是一座M层的大楼,1<=M<=100。每层楼都有N个办公室,编号为1..N(1<=N<=500)。每个办公室有一个签证员。签证需要让第M层的某个签证员盖章才有效。每个签证员都要满足下面三个条件之一才会给xuzhenyi盖章:
1. 这个签证员在1楼
2. xuzhenyi的签证已经给这个签证员的正楼下(房间号相同)的签证员盖过章了。
3. xuzhenyi的签证已经给这个签证员的相邻房间(房间号相差1,楼层相同)的签证员盖过章了。
每个签证员盖章都要收取一定费用,这个费用不超过1000000000。找出费用最小的盖章路线,使签证生效
二、分析
DP顺序:从下到上,再从左到右,再从右到左,与上题一样,为了保证其无后效性,所以同一层的需要分开扫描
坐标型DP。设计一个状态f[i,j]为找第i层第j个签证员所要花费的总费用。
状态转移很明显。
f[i,j]:=min{f[i-1,j]+a[i,j];f[i,j-1]+a[i,j];f[i,j+1]+a[i,j];}
只是f[i,j-1]和f[i,j+1]不能够在同一次循环中全部求出来,所以要扫两次。
记录路径:用x和y分别记录
马拦卒过河noip2002
一、问题描述:棋盘上A点有一个过河卒,需要走到目标B点。卒行走的规则:可以向下、或者向右。同时在棋盘上C点有一个对方的马,该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。棋盘用坐标表示,A点(0, 0)、B点(n, m)(n, m为不超过15的整数),同样马的位置坐标是需要给出的。现在要求你计算出卒从A点能够到达B点的路径的条数,假设马的位置是固定不动的,并不是卒走一步马走一步。
二、分析:就是简单考虑路径,但是这里需要注意的一个是马的地方不能走,这个特判下就好了,还有就是边界条件,如果马走了边界,那么边界要注意赋值为前一个
打砖块(tyvj’1505)
一、 问题描述:
在一个凹槽中放置了n层砖块、最上面的一层有n 块砖,从上到下每层依次减少一块砖。每块砖都有一个分值,敲掉这块砖就能得到相应的分值,如下图所示。
14 15 4 3 23
33 33 76 2
2 13 11
22 23
31
如果你想敲掉第i层的第j块砖的话,若i=1,你可以直接敲掉它;若i>1,则你必须先敲掉第i-1层的第j和第j+1块砖。
你现在可以敲掉最多m块砖,求得分最多能有多少。
二分析:
f[i,j,k]表示,到了第i行,总共取j个,在第i行取k个用g[i,j,k]数组记录从f[i,j,k]到f[i,j,i]中的最大值,用s[i,j]记录转换后的第i行前j个数的和
方程:f[i,j,k]=g[i-1,j-k,k-1]+s[i,k];
把三角形倒过来了!
比如说样例:
2 2 3 4
8 2 7
2 3
49
倒过来之后——>
4
3 7
2 2 3
2 8 2 49
那么每一点只能由左边的点转移过来,和左上角一直到上一行末尾的数转移过来。
如第四行第2个数可以从第三行的1,2,3个数转移过来。为什么?再回去看看题吧……
此题就是典型的区间DP,先搬砖块都变成直角三角形,然后分析阶段和边界,通过题里的叙述很容易推出递推公式:f[i][j][k]=f[i][j][k]+a[v][i];
边界:f[n+1][0][0]=0;
目标:f[i][j][k];
从右向左推,f[i,j,k]表示第i列敲掉j个砖头一共敲掉k个砖头所得到的最优值。第i列敲掉j个砖头,则第i+1列就至少要敲掉j-1个砖头。第i列一共要敲掉k个,第i+1列及其以前就要敲掉k-j个砖头。
f[i,j,k]:=max(f[i+1,v,k-j])+sum[j,i];(j-1<=v<=n-i)
sum[j,i]表示第i列,从第1行到第j行所有砖头的值的和
注意边界条件,赋初值要赋一个很大的负数。然后把f[n+1,0,0]赋成0
0<=j<=n-i+1,j<=k<=m
注意:j应该从0开始,而不能从1开始,因为该列可以一个也不取,而这个状态应该被保存,否则不一定达到最优。
打鼹鼠(CscIIvijos 1441)
一、问题描述:阿Q编写了一个打鼹鼠的游戏:在一个n*n的网格中,在某些时刻鼹鼠会在某一个网格探出头来透透气。你可以控制一个机器人来打鼹鼠,如果i时刻鼹鼠在某个网格中出现,而机器人也处于同一网格的话,那么这个鼹鼠就会被机器人打死。而机器人每一时刻只能够移动一格或停留在原地不动。机器人的移动是指从当前所处的网格移向相邻的网格,即从坐标为(i,j)的网格移向(i-1, j),(i+1, j),(i,j-1),(i,j+1)四个网格,机器人不能走出整个n*n的网格。游戏开始时,你可以自由选定机器人的初始位置。现在你知道在一段时间内,鼹鼠出现的时间和地点,希望你编写一个程序使机器人在这一段时间内打死尽可能多的鼹鼠。
输入格式:文件第一行为n(n<=1000), m(m<=10000),其中m表示在这一段时间内出现的鼹鼠的个数,接下来的m行每行有三个数据time,x,y表示有一只鼹鼠在游戏开始后time个时刻,在第x行第y个网格里出现了一只鼹鼠。Time按递增的顺序给出。注意同一时刻可能出现多只鼹鼠,但同一时刻同一地点只可能出现多只鼹鼠。
输出格式:输出文件中仅包含一个正整数,表示被打死鼹鼠的最大数目。
二、分析:分析:经典DP题。这题一开始很容易想到一个(n^2t)的算法,定义dp[i][j][k]表示在第i秒,站在点(j,k)上所能打到的最多鼹鼠数目,方程也很好列。可惜n最多要有1000,而且k也不小,使用这个方法必定超时+超内存。仔细分析此题,发现假如机器人要移动到某个位置,那么它一定是走一条最短路径(其实就是曼哈顿距离,公式distance=|x1-x2|+|y1-y2|)否则解就不一定是最优的。还有,假如在某个点打死了一个地鼠,那么机器人的位置一定是站在那个死掉地鼠出现的位置上。这样我们就可以想出一个新的状态表示方法:定义dp[i]表示对于前i只鼹鼠,最多能打死多少只,而且当前机器人站在i号鼹鼠的位置。这样方程就类似于LCS问题,也就是对于当前的鼹鼠位置,枚举机器人上一次打死鼹鼠的地方,判断这两个地方是否可以到达,如果可以到达那么dp[i]+1,否则continue。
这里有一个小优化:在枚举鼹鼠位置的时候可以倒着枚举,这样简单的常数优化居然提高了1.2s的程序运行速度!
贪吃的九头龙(NOI2002)
一、问题描述:传说中的九头龙是一种特别贪吃的动物。虽然名字叫“九头龙”,但这只是说它出生的时候有九个头,而在成长的过程中,它有时会长出很多的新头,头的总数会远大于九,当然也会有旧头因衰老而自己脱落。
有一天,有M个脑袋的九头龙看到一棵长有N个果子的果树,喜出望外,恨不得一口把它全部吃掉。可是必须照顾到每个头,因此它需要把N个果子分成M组,每组至少有一个果子,让每个头吃一组。
这M个脑袋中有一个最大,称为“大头”,是众头之首,它要吃掉恰好K个果子,而且K个果子中理所当然地应该包括唯一的一个最大的果子。果子由N-1根树枝连接起来,由于果树是一个整体,因此可以从任意一个果子出发沿着树枝“走到”任何一个其他的果子。
对于每段树枝,如果它所连接的两个果子需要由不同的头来吃掉,那么两个头会共同把树枝弄断而把果子分开;如果这两个果子是由同一个头来吃掉,那么这个头会懒得把它弄断而直接把果子连同树枝一起吃掉。当然,吃树枝并不是很舒服的,因此每段树枝都有一个吃下去的“难受值”,而九头龙的难受值就是所有头吃掉的树枝的“难受值”之和。
九头龙希望它的“难受值”尽量小,你能帮它算算吗?
二、分析
题目简述:将一棵树中的节点染成M种颜色,每个节点有且只有一种颜色,在满足以下条件下使得两端颜色相同的边的权值和最小,所有边权均非负。(1)必须有K个1号颜色的点;(2)1号节点必须是1号颜色;(3)每种颜色必须至少有一个节点。如无解,输-1。
无解的情况很明显,当且仅当N-K<M-1时无解。有解的考虑用动态规划来解决。
如果以一棵子树作为一个子结构,分析需要考虑的状态:
(1)根节点的颜色。(2)1号颜色的个数。(3)树中颜色的分配情况,如何保证每种颜色都有节点。
初步分析可以得到一种四维的状态:
f[i][j][k][w],表示在以i为根的子树中,有j个1号节点,根染k号颜色,树中已有的颜色用w表示(w是一个二进制数)的状态下最小的权值和。
首先,这个方程用到了状态压缩w,因此对于本题300的数据范围是不现实的,需要继续思考。
假设这样一个问题,仍然是对树染色,可以任意染色,那么只要2种颜色,就可以保证任意一条边两端的颜色不同,联想到这道题,因为1号颜色比较特殊,因此单独处理,而余下的颜色如果大于等于2种,那么无论1号颜色如何染色,都可以保证一条边两边不会出现相同的非1号颜色的情况,换言之,如果M>=3,对答案有贡献的只有1号颜色节点之间的边。这样当M>=3时,可以直接按3处理,这样状态压缩是可以承受的。既然有了这样的优化,k也可以只用0,1来