【OpenCV学习笔记 020】K-Means聚类算法介绍及实现
一、K-Means算法介绍
在数据挖掘中,K-Means算法是一种cluster analysis的算法,其主要是来计算数据聚集的算法,主要通过不断地取离种子点最近均值的算法。
问题
K-Means算法主要解决的问题如下图所示。我们可以看到,在图的左边有一些点,我们用肉眼可以看出来有四个点群,但是我们怎么通过计算机程序找出这几个点群来呢?于是就出现了我们的K-Means算法(Wikipedia链接)

K-Means要解决的问题
算法概要:
这个算法其实很简单,如下图所示:

从上图中,我们可以看到,A,B,C,D,E是五个在图中点。而灰色的点是我们的种子点,也就是我们用来找点群的点。有两个种子点,所以K=2。
然后,K-Means的算法如下:
- 随机在图中取K(这里K=2)个种子点。
- 然后对图中的所有点求到这K个种子点的距离,假如点Pi离种子点Si最近,那么Pi属于Si点群。(上图中,我们可以看到A,B属于上面的种子点,C,D,E属于下面中部的种子点)
- 接下来,我们要移动种子点到属于他的“点群”的中心。(见图上的第三步)
- 然后重复第2)和第3)步,直到,种子点没有移动(我们可以看到图中的第四步上面的种子点聚合了A,B,C,下面的种子点聚合了D,E)。
这个算法很简单,但是有些细节我要提一下,求距离的公式我不说了,大家有初中毕业水平的人都应该知道怎么算的。我重点想说一下“求点群中心的算法”。
求点群中心的算法
一般来说,求点群中心点的算法你可以很简单的使用各个点的X/Y坐标的平均值。不过,我这里想告诉大家另三个求中心点的的公式:
1)Minkowski Distance公式——λ可以随意取值,可以是负数,也可以是正数,或是无穷大。

2)Euclidean Distance公式——也就是第一个公式λ=2的情况

3)CityBlock Distance公式——也就是第一个公式λ=1的情况
![]()
这三个公式的求中心点有一些不一样的地方,我们看下图(对于第一个λ在0-1之间)。



(1)Minkowski Distance (2)Euclidean Distance (3) CityBlock Distance
上面这几个图的大意是他们是怎么个逼近中心的,第一个图以星形的方式,第二个图以同心圆的方式,第三个图以菱形的方式。K-Means的演示
如果你以”K Means Demo“为关键字到Google里查你可以查到很多演示。这里推荐一个演示:http://home.dei.polimi.it/matteucc/Clustering/tutorial_html/AppletKM.html
操作是,鼠标左键是初始化点,右键初始化“种子点”,然后勾选“Show History”可以看到一步一步的迭代。
注:这个演示的链接也有一个不错的K Means Tutorial。
K-Means++算法
K-Means主要有两个最重大的缺陷——都和初始值有关:
- K是事先给定的,这个K值的选定是非常难以估计的。很多时候,事先并不知道给定的数据集应该分成多少个类别才最合适。(ISODATA算法通过类的自动合并和分裂,得到较为合理的类型数目K)
- K-Means算法需要用初始随机种子点来搞,这个随机种子点太重要,不同的随机种子点会有得到完全不同的结果。(K-Means++算法可以用来解决这个问题,其可以有效地选择初始点)
我在这里重点说一下K-Means++算法步骤:
- 先从我们的数据库随机挑个随机点当“种子点”。
- 对于每个点,我们都计算其和最近的一个“种子点”的距离D(x)并保存在一个数组里,然后把这些距离加起来得到Sum(D(x))。
- 然后,再取一个随机值,用权重的方式来取计算下一个“种子点”。这个算法的实现是,先取一个能落在Sum(D(x))中的随机值Random,然后用Random -= D(x),直到其<=0,此时的点就是下一个“种子点”。
- 重复第(2)和第(3)步直到所有的K个种子点都被选出来。
- 进行K-Means算法。
相关的代码你可以在这里找到“implement the K-means++ algorithm”(墙)另,Apache的通用数据学库也实现了这一算法
K-Means算法应用
看到这里,你会说,K-Means算法看来很简单,而且好像就是在玩坐标点,没什么真实用处。而且,这个算法缺陷很多,还不如人工呢。是的,前面的例子只是玩二维坐标点,的确没什么意思。但是你想一下下面的几个问题:
1)如果不是二维的,是多维的,如5维的,那么,就只能用计算机来计算了。
2)二维坐标点的X,Y 坐标,其实是一种向量,是一种数学抽象。现实世界中很多属性是可以抽象成向量的,比如,我们的年龄,我们的喜好,我们的商品,等等,能抽象成向量的目的就是可以让计算机知道某两个属性间的距离。如:我们认为,18岁的人离24岁的人的距离要比离12岁的距离要近,鞋子这个商品离衣服这个商品的距离要比电脑要近,等等。
只要能把现实世界的物体的属性抽象成向量,就可以用K-Means算法来归类了。
在《k均值聚类(K-means)》 这篇文章中举了一个很不错的应用例子,作者用亚洲15支足球队的2005年到1010年的战绩做了一个向量表,然后用K-Means把球队归类,得出了下面的结果,呵呵。
- 亚洲一流:日本,韩国,伊朗,沙特
- 亚洲二流:乌兹别克斯坦,巴林,朝鲜
- 亚洲三流:中国,伊拉克,卡塔尔,阿联酋,泰国,越南,阿曼,印尼
其实,这样的业务例子还有很多,比如,分析一个公司的客户分类,这样可以对不同的客户使用不同的商业策略,或是电子商务中分析商品相似度,归类商品,从而可以使用一些不同的销售策略,等等。
最后给一个挺好的算法的幻灯片:http://www.cs.cmu.edu/~guestrin/Class/10701-S07/Slides/clustering.pdf
二、OpenCV自带samples中kmeans研究
实验基础
在使用kmeans之前,必须先了解kmeans算法的2个缺点:第一是必须人为指定所聚的类的个数k;第二是如果使用欧式距离来衡量相似度的话,可能会得到错误的结果,因为没有考虑到属性的重要性和相关性。为了减少这种错误,在使用kmeans距离时,一定要使样本的每一维数据归一化,不然的话由于样本的属性范围不同会导致错误的结果。
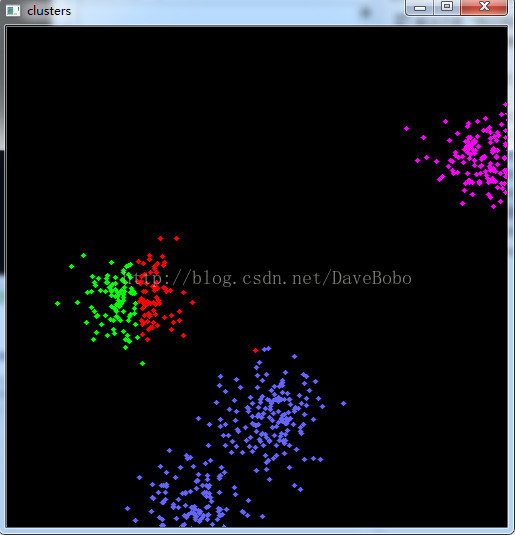
实验一是对随机产生的sampleCount个二维样本(共分为clusterCount个类别),每个类别的样本数据都服从高斯分布,该高斯分布的均值是随机的,方差是固定的。然后对这sampleCount个样本数据使用kmeans算法聚类,最后将不同的类用不同的颜色显示出来。
下面是程序中使用到的几个OpenCV函数:
void RNG::fill(InputOutputArray mat, int distType, InputArray a,InputArray b, bool saturateRange=false )这个函数是对矩阵mat填充随机数,随机数的产生方式有参数2来决定,如果为参数2的类型为RNG::UNIFORM,则表示产生均一分布的随机数,如果为RNG::NORMAL则表示产生高斯分布的随机数。对应的参数3和参数4为上面两种随机数产生模型的参数。比如说如果随机数产生模型为均匀分布,则参数a表示均匀分布的下限,参数b表示上限。如果随机数产生模型为高斯模型,则参数a表示均值,参数b表示方程。参数5只有当随机数产生方式为均匀分布时才有效,表示的是是否产生的数据要布满整个范围(没用过,所以也没仔细去研究)。另外,需要注意的是用来保存随机数的矩阵mat可以是多维的,也可以是多通道的,目前最多只能支持4个通道。
void randShuffle(InputOutputArray dst, double iterFactor=1., RNG*rng=0 )该函数表示随机打乱1D数组dst里面的数据,随机打乱的方式由随机数发生器rng决定。iterFactor为随机打乱数据对数的因子,总共打乱的数据对数为:dst.rows*dst.cols*iterFactor,因此如果为0,表示没有打乱数据。
Class TermCriteria
类TermCriteria 一般表示迭代终止的条件,如果为CV_TERMCRIT_ITER,则用最大迭代次数作为终止条件,如果为CV_TERMCRIT_EPS 则用精度作为迭代条件,如果为CV_TERMCRIT_ITER+CV_TERMCRIT_EPS则用最大迭代次数或者精度作为迭代条件,看哪个条件先满足。
double kmeans(InputArray data, int K, InputOutputArray bestLabels,TermCriteria criteria, int attempts, int flags, OutputArray centers=noArray() )
该函数为kmeans聚类算法实现函数。参数data表示需要被聚类的原始数据集合,一行表示一个数据样本,每一个样本的每一列都是一个属性;参数k表示需要被聚类的个数;参数bestLabels表示每一个样本的类的标签,是一个整数,从0开始的索引整数;参数criteria表示的是算法迭代终止条件;参数attempts表示运行kmeans的次数,取结果最好的那次聚类为最终的聚类,要配合下一个参数flages来使用;参数flags表示的是聚类初始化的条件。其取值有3种情况,如果为KMEANS_RANDOM_CENTERS,则表示为随机选取初始化中心点,如果为KMEANS_PP_CENTERS则表示使用某一种算法来确定初始聚类的点;如果为KMEANS_USE_INITIAL_LABELS,则表示使用用户自定义的初始点,但是如果此时的attempts大于1,则后面的聚类初始点依旧使用随机的方式;参数centers表示的是聚类后的中心点存放矩阵。该函数返回的是聚类结果的紧凑性,其计算公式为:

实验一:随机产生的符合高斯分布的数据被聚类的结果
实验代码及注释
#include "opencv2/highgui/highgui.hpp"
#include "opencv2/core/core.hpp"
#include <iostream>
using namespace cv;
using namespace std;
// static void help()
// {
// cout << "
This program demonstrates kmeans clustering.
"
// "It generates an image with random points, then assigns a random number of cluster
"
// "centers and uses kmeans to move those cluster centers to their representitive location
"
// "Call
"
// "./kmeans
" << endl;
// }
int main(int /*argc*/, char** /*argv*/)
{
const int MAX_CLUSTERS = 5;
Scalar colorTab[] = //因为最多只有5类,所以最多也就给5个颜色
{
Scalar(0, 0, 255),
Scalar(0, 255, 0),
Scalar(255, 100, 100),
Scalar(255, 0, 255),
Scalar(0, 255, 255)
};
Mat img(500, 500, CV_8UC3);
RNG rng(12345); //随机数产生器
for (;;)
{
int k, clusterCount = rng.uniform(2, MAX_CLUSTERS + 1);
int i, sampleCount = rng.uniform(1, 1001);
Mat points(sampleCount, 1, CV_32FC2), labels; //产生的样本数,实际上为2通道的列向量,元素类型为Point2f
clusterCount = MIN(clusterCount, sampleCount);
Mat centers(clusterCount, 1, points.type()); //用来存储聚类后的中心点
/* generate random sample from multigaussian distribution */
for (k = 0; k < clusterCount; k++) //产生随机数
{
Point center;
center.x = rng.uniform(0, img.cols);
center.y = rng.uniform(0, img.rows);
Mat pointChunk = points.rowRange(k*sampleCount / clusterCount,
k == clusterCount - 1 ? sampleCount :
(k + 1)*sampleCount / clusterCount); //最后一个类的样本数不一定是平分的,
//剩下的一份都给最后一类
//每一类都是同样的方差,只是均值不同而已
rng.fill(pointChunk, CV_RAND_NORMAL, Scalar(center.x, center.y), Scalar(img.cols*0.05, img.rows*0.05));
}
randShuffle(points, 1, &rng); //因为要聚类,所以先随机打乱points里面的点,注意points和pointChunk是共用数据的。
kmeans(points, clusterCount, labels,
TermCriteria(CV_TERMCRIT_EPS + CV_TERMCRIT_ITER, 10, 1.0),
3, KMEANS_PP_CENTERS, centers); //聚类3次,取结果最好的那次,聚类的初始化采用PP特定的随机算法。
img = Scalar::all(0);
for (i = 0; i < sampleCount; i++)
{
int clusterIdx = labels.at<int>(i);
Point ipt = points.at<Point2f>(i);
circle(img, ipt, 2, colorTab[clusterIdx], CV_FILLED, CV_AA);
}
imshow("clusters", img);
char key = (char)waitKey(); //无限等待
if (key == 27 || key == "q" || key == "Q") // "ESC"
break;
}
return 0;
}
实验二是对输入的一张图片进行聚类。
实验代码及注释
#include<core/core.hpp>
#include<highgui/highgui.hpp>
#include<imgproc/imgproc.hpp>
#include<ml/ml.hpp>
using namespace std;
using namespace cv;
int main(int argc, char **argv)
{
/*if (argc<3)
return -1;
Mat Img = imread(argv[1], IMREAD_COLOR);
const int K = atoi(argv[2]);*/
Mat Img = imread("beach.jpg", IMREAD_COLOR);//源图像
const int K = 8;//聚类个数
if (Img.empty() || K <= 0)
return -1;
Mat ImgHSV;
cvtColor(Img, ImgHSV, CV_BGR2HSV);//将RGB空间转换为HSV空间
Mat ImgData(Img.rows*Img.cols, 1, CV_32FC3);//一个3通道的数据域
Mat_<Vec3b>::iterator itImg = ImgHSV.begin<Vec3b>();//迭代器
Mat_<Vec3f>::iterator itData = ImgData.begin<Vec3f>();
//将源图像的数据输入给新建的ImgData
for (; itImg != ImgHSV.end<Vec3b>(); ++itImg, ++itData)
*itData = *itImg;
Mat ImgLabel, ImgCenter;
kmeans(ImgData, K, ImgLabel, TermCriteria(CV_TERMCRIT_EPS + CV_TERMCRIT_ITER, 10, 1.0), 1, KMEANS_PP_CENTERS, ImgCenter);
Mat ImgRes(Img.size(), CV_8UC3);
Mat_<Vec3b>::iterator itRes = ImgRes.begin<Vec3b>();
Mat_<int>::iterator itLabel = ImgLabel.begin<int>();
for (; itLabel != ImgLabel.end<int>(); ++itLabel, ++itRes)
*itRes = ImgCenter.at<Vec3f>(*itLabel, 0);
//cout << ImgCenter << endl;
cvtColor(ImgRes, ImgRes, CV_HSV2BGR);
imwrite("out.jpg", ImgRes);
namedWindow("Img", WINDOW_AUTOSIZE);
imshow("Img", Img);
namedWindow("Res", WINDOW_AUTOSIZE);
imshow("Res", ImgRes);
waitKey();
return 0;
}源图像:
聚类后的图像:
三、OpenCV的Kmean算法实践
首先看一下opencv中kmeans的函数原型
//! clusters the input data using k-Means algorithm
CV_EXPORTS_W double kmeans( InputArray data, int K, CV_OUT InputOutputArray bestLabels,
TermCriteria criteria, int attempts,
int flags, OutputArray centers=noArray() );data:输入样本,要分类的对象,浮点型,每行一个样本(我要对颜色分类则每行一个像素);K: 类型数目;
bestLabels: 分类后的矩阵,每个样本对应一个类型label;
TermCriteria criteria:结束条件(最大迭代数和理想精度)
int attempts:根据最后一个参数确定选取的最理想初始聚类中心(选取attempt次初始中心,选择compactness最小的);
int flags :
Flag that can take the following values:
KMEANS_RANDOM_CENTERS Select random initial centers in each attempt.
KMEANS_PP_CENTERS Use kmeans++ center initialization by Arthur and Vassilvitskii [Arthur2007].
KMEANS_USE_INITIAL_LABELS During the first (and possibly the only) attempt, use the user-supplied labels instead of computing them from the initial centers. For the second and further attempts, use the random or semi-random centers. Use one of KMEANS_*_CENTERS
flag to specify the exact method.
centers:输出聚类中心,每行一个中心
compactness: 测试初始中心是否最优
程序源码:
#include <string>
#include <iostream>
#include <math.h>
#include <vector>
#include <map>
#include "opencv/cv.h"
#include "opencv/highgui.h"
#include "opencv/cxcore.h"
#define ClusterNum 6
using namespace cv;
using namespace std;
string fileName = "image.jpg";
Mat clustering(Mat src){
int row = src.rows;
int col = src.cols;
unsigned long int size = row*col;
Mat clusters(size, 1, CV_32SC1); //clustering Mat, save class label at every location;
//convert src Mat to sample srcPoint.
Mat srcPoint(size, 1, CV_32FC3);
Vec3f* srcPoint_p = (Vec3f*)srcPoint.data;
Vec3f* src_p = (Vec3f*)src.data;
unsigned long int i;
for (i = 0; i < size;i++)
{
*srcPoint_p = *src_p;
srcPoint_p++;
src_p++;
}
Mat center(ClusterNum, 1, CV_32FC3);
double compactness;//compactness to measure the clustering center dist sum by different flag
compactness = kmeans(srcPoint, ClusterNum, clusters,
cvTermCriteria(CV_TERMCRIT_EPS + CV_TERMCRIT_ITER, 10, 0.1), ClusterNum,
KMEANS_PP_CENTERS, center);
cout << "center row:" << center.rows << " col:" << center.cols << endl;
for (int y = 0; y < center.rows; y++)
{
Vec3f* imgData = center.ptr<Vec3f>(y);
for (int x = 0; x < center.cols; x++)
{
cout << imgData[x].val[0] << " " << imgData[x].val[1] << " " << imgData[x].val[2] << endl;
}
cout << endl;
}
double minH, maxH;
minMaxLoc(clusters, &minH, &maxH); //remember must use
cout << "H-channel min:" << minH << " max:" << maxH << endl;
int* clusters_p = (int*)clusters.data;
//show label mat
Mat label(src.size(), CV_32SC1);
int* label_p = (int*)label.data;
//assign the clusters to Mat label
for (i = 0; i < size; i++)
{
*label_p = *clusters_p;
label_p++;
clusters_p++;
}
Mat label_show;
label.convertTo(label_show, CV_8UC1);
normalize(label_show, label_show, 255, 0, CV_MINMAX);
imshow("label", label_show);
map<int, int> count; //map<id,num>
map<int, Vec3f> avg; //map<id,color>
//compute average color value of one label
for (int y = 0; y < row; y++)
{
const Vec3f* imgData = src.ptr<Vec3f>(y);
int* idx = label.ptr<int>(y);
for (int x = 0; x < col; x++)
{
avg[idx[x]] += imgData[x];
count[idx[x]] ++;
}
}
//output the average value (clustering center)
//计算所得的聚类中心与kmean函数中center的第一列一致,
//以后可以省去后面这些繁复的计算,直接利用center,
//但是仍然不理解center的除第一列以外的其他列所代表的意思
for (i = 0; i < ClusterNum; i++)
{
avg[i] /= count[i];
if (avg[i].val[0]>0 && avg[i].val[1]>0 && avg[i].val[2]>0)
{
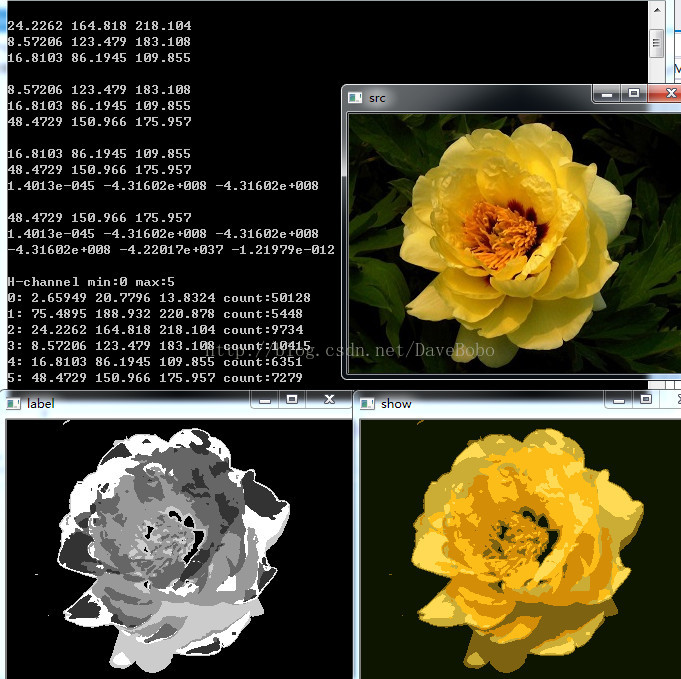
cout << i << ": " << avg[i].val[0] << " " << avg[i].val[1] << " " << avg[i].val[2] << " count:" << count[i] << endl;
}
}
//show the clustering img;
Mat showImg(src.size(), CV_32FC3);
for (int y = 0; y < row;y++)
{
Vec3f* imgData = showImg.ptr<Vec3f>(y);
int *idx = label.ptr<int>(y);
for (int x = 0; x < col;x++)
{
int id = idx[x];
imgData[x].val[0] = avg[id].val[0];
imgData[x].val[1] = avg[id].val[1];
imgData[x].val[2] = avg[id].val[2];
}
}
normalize(showImg, showImg, 1, 0, CV_MINMAX);
imshow("show", showImg);
waitKey();
return label;
}
int main(){
Mat img = imread(fileName, 1);
imshow("src", img);
GaussianBlur(img, img, Size(3, 3), 0);
img.convertTo(img, CV_32FC3);
Mat pixId = clustering(img);
}
实验结果:
Refrence
http://www.csdn.net/article/2012-07-03/2807073-k-means
http://www.cnblogs.com/moondark/archive/2012/03/08/2385770.html
http://blog.csdn.net/yangtrees/article/details/7971405
http://blog.csdn.net/ts_zxc/article/details/23668751
http://www.opencv.org.cn/opencvdoc/2.3.2/html/modules/core/doc/clustering.html#kmeans
如果文章对更多的朋友有益,请分享到朋友圈。【视音频图像技术干货,FFmpeg流媒体、OpenCV图像及深度学习技术探索,开源项目推荐,还有更多职场规划】欢迎关注我的微信公众号,扫一扫下方二维码或者长按识别二维码。