RSA加密算法(C语言实现)
这次轮到RSA加密算法了。RSA加密过程相对DES和MD5要简单很多,但作为现在还在使用的加密算法之一,它还是有需要认真思索的地方哒~
首先是密钥对的生成:
(1)选取两个大素数p和q(目前两个数的长度都接近512bit是安全的)
(2)计算乘积n=p*q,Φ(n)=(p-1)(q-1),其中Φ(n)为n的欧拉函数(因为两素数乘积的欧拉函数等于两数分别减一后的乘积)
(3)随机选取整数e(1<e<Φ(n))作为公钥d,要求满足e与Φ(n)的最大公约数为1,即两者互素
(4)用Euclid扩展算法计算私钥d,已满足d * e ≡ 1 (mod Φ(n)),即d ≡ e^(-1) (mod Φ(n))。则e与n是公钥,d是私钥
注意:e与n应公开,两个素数p和q不再需要,可销毁,但绝不可泄露。
加密过程:
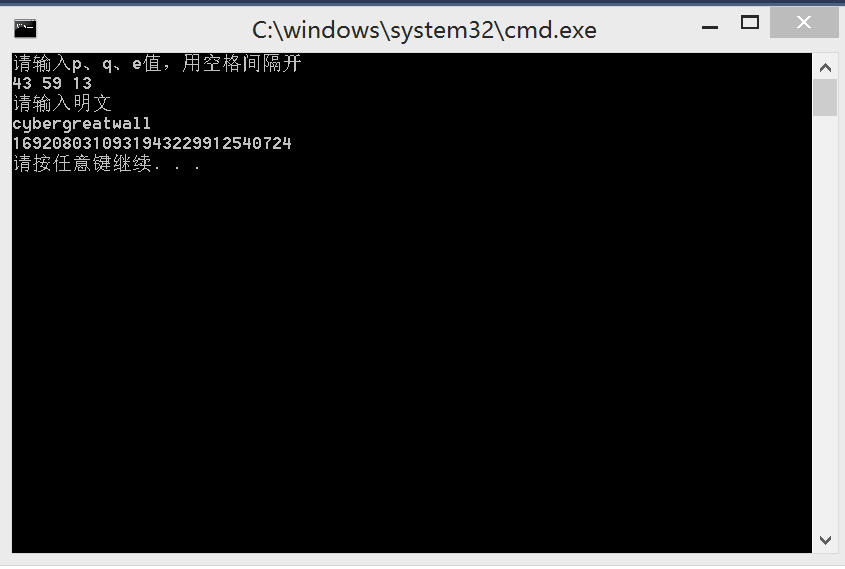
将接收到的明文转换成特定的编码方式。如p=43,q=59,e=13,明文为cybergreatwall,按照英文字母表的顺序a=00,b=01,... ,z=25进行编码后为022401041706001922001111。
然后将转码后的字符串分块,分组要求:每个分组对应的十进制数小于0。这个要求是什么意思呢?我个人的理解通过举例向大家说明:上文字符串分组如下0224 0104 1706 0019 2200 1111。每一分组的数都小于n(2537),而2537能接受的最大的数为2525(也就是‘zz’的情况),所以是4位1组,即两字符一组。这样一来,m1=0224,m2=0104,... ,m6=1111
现在可以加密了~~加密算法就是这个式子----ci ≡ mi^e (mod n),如第一分组 0224^13 ≡ mod 2537 ≡ 1692=c1 。这里有个隐藏的算法是需要了解的:
在RSA算法过程中容易出现天文数字(像上文的0224^13),而这些天文数字会为我们编程的过程造成一定的麻烦,更可恶的是会影响速度!!为了避免这种情况,快速取模指数算法可以很有效地算出c≡m^e mod n的准确结果且避免过程中出现天文数字~~
下面用伪代码为大家介绍下这种神奇的算法(个人感觉伪代码里的 ‘<-’ 就是平时用的 ‘=’ ):
t<-0;c<-1
for i<-k downto 0
do t<-2*t
c<-(c*c)mod n
if bi=1 then t<-t+1
c<-(c*m)mod n
return c
(p.s:e的二进制表示为bk bk-1 ... b0,如e=13=(1101),所以k为3)
所以,用快速取模指数算法计算上文例子里的c1过程就该是这样子哒:
i 3 2 1 0
bi 1 1 0 1
t 1 3 6 13
ci (1*224)mod2537 (224*224*224)mod2537 (514*514)mod2537 (348*348*224)mod2537
=224 =514 =348 =1692
到这里RSA加密的算法就讲完了,下面附上代码
#include<stdio.h>
#include<stdlib.h>
/* 函数申明 */
int long_n(int n);
int shuru(char *arr, int k, char *wei, int is_first);
void jiami(char *arr, int k, int e, int n);
/* 输入函数,记录从键盘输入的明文*/
int shuru(char *arr, int k, char *wei, int is_first)
{
int i;
char ch;
/*判断是否为第一分组的输入,如果是则获取输入的字符,否则就将上一分组最后获取的字符作为这一分组的第一个字符*/
if (is_first == 1)
ch = getchar();
else
ch = *wei;
for (i = 0; (i < k) && (ch != "
");i++) //获取字符直到获取到回车符为止
{
arr[i] = ch;
ch = getchar();
}
*wei = ch; //最后获取到的字符准备作为下一分组的第一个字符
for (i = i; i < k; i++)
arr[i] = "a"; //输入不够一组个数的整数倍则补"a"(即为补零)
if (ch == "
") //接收到回车符返回0,否则为1
return 0;
else
return 1;
}
/*加密函数*/
void jiami(char *arr, int k, int e, int n)
{
int m = 0,c=1, i, j,t=0, shu,temp,num=0;
int *array;
/*Mi赋值过程*/
for (i = 0; i < k; i++)
{
temp = 1;
for (j = 0; j < (k-i-1)*2; j++)
temp = temp * 10;
shu = (int)arr[i] - 97;
m = m + temp * shu;
}
temp = e;
/*获取e的二进制表达形式的位数*/
do{
temp = temp / 2;
num++;
} while (temp != 0);
array = (int *)malloc(sizeof(int)*k); //申请动态数组
temp = e;
/*动态数组存储e的二进制表达形式*/
for (i = 0; i < num; i++)
{
array[i] = temp % 2;
temp = temp / 2;
}
/*避免出现天文数字的算法,详情见上文文字说明*/
for (i = num - 1; i >= 0; i--)
{
t = t * 2;
temp = c*c;
if (temp > n)
{
for (j = 0; temp - n*j >= 0; j++);
j--;
c = temp - n*j;
}
else
c = temp;
if (array[i] == 1)
{
t = t + 1;
temp = c*m;
if (temp > n)
{
for (j = 0; temp - n*j >= 0; j++);
j--;
c = temp - n*j;
}
else
c = temp;
}
e = e / 2;
}
temp = c;
i = 0;
/*c的位数小于分组长度则在前补零*/
do{
temp = temp / 10;
i++;
} while (temp != 0);
for (i; i < num; i++)
printf("0");
printf("%d", c);
}
/*获取分组的长度*/
int long_n(int n)
{
int temp,i,j,k,shi,comp=0;
temp = n;
/*获取n的位数*/
for (i = 1; temp / 10 != 0; i++)
{
temp = temp / 10;
}
temp = i;
/*若n的位数为基数*/
if (i % 2 != 0)
{
i = i - 1;
return i;
}
/*若位数为偶数*/
else
{
for (j = 0; j < i/2; j++)
{
shi = 1;
for (k = 0; k < temp - 2; k++)
shi = shi * 10;
comp = comp + shi * 25;
temp = temp - 2;
}
if (comp <= n)
return i;
else
{
i = i - 2;
return i;
}
}
}
/*主函数*/
int main()
{
int p, q, e, d, n, fai_n, k, i,is_first=1;
char ch,*arr,wei="a";
printf("请输入p、q、e值,用空格间隔开
");
scanf_s("%d%d%d", &p, &q, &e); //从键盘获取p、q、e值
n = p*q;
fai_n = (p-1)*(q-1); //Φ(n)
for (k = 0; (k*n + 1) % e != 0; k++);
if ((k*n + 1) % e == 0)
d = (k*n + 1) / e; //d * e ≡ 1 (mod Φ(n))
k = long_n(n);
k = k / 2; //分组的长度
ch = getchar(); //缓冲回车符
arr = (char *)malloc(sizeof(char)*k); //申请动态数组
printf("请输入明文
");
while (1)
{
i=shuru(arr,k,&wei,is_first); //调用输入字符的函数,接收到回车符返回0,否则为1
is_first = 0; //第一分组录入结束设为0
jiami(arr,k,e,n); //调用加密函数
if (i == 0) //接收到返回值为0跳出循环
break;
}
printf("
");
return 0;
}运行结果:
如果有对算法和代码不理解或者有不同看法的请联系我哦,邮箱在我的信息里~~
- 上一篇: RSA加密算法例子解读
- 下一篇: RSA加密算法详解