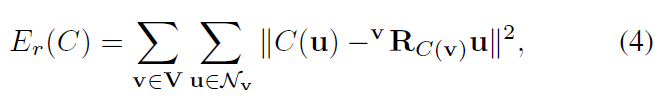qianyi-zhou offline RGB-D 三维重建(2)
接着上篇博客讨论,上篇博客:
http://blog.csdn.net/fuxingyin/article/details/52926154
这篇博客先介绍“Elastic Fragments for Dense Scene Reconstruction”,后续再介绍比较相关的一篇文章。
先上图:
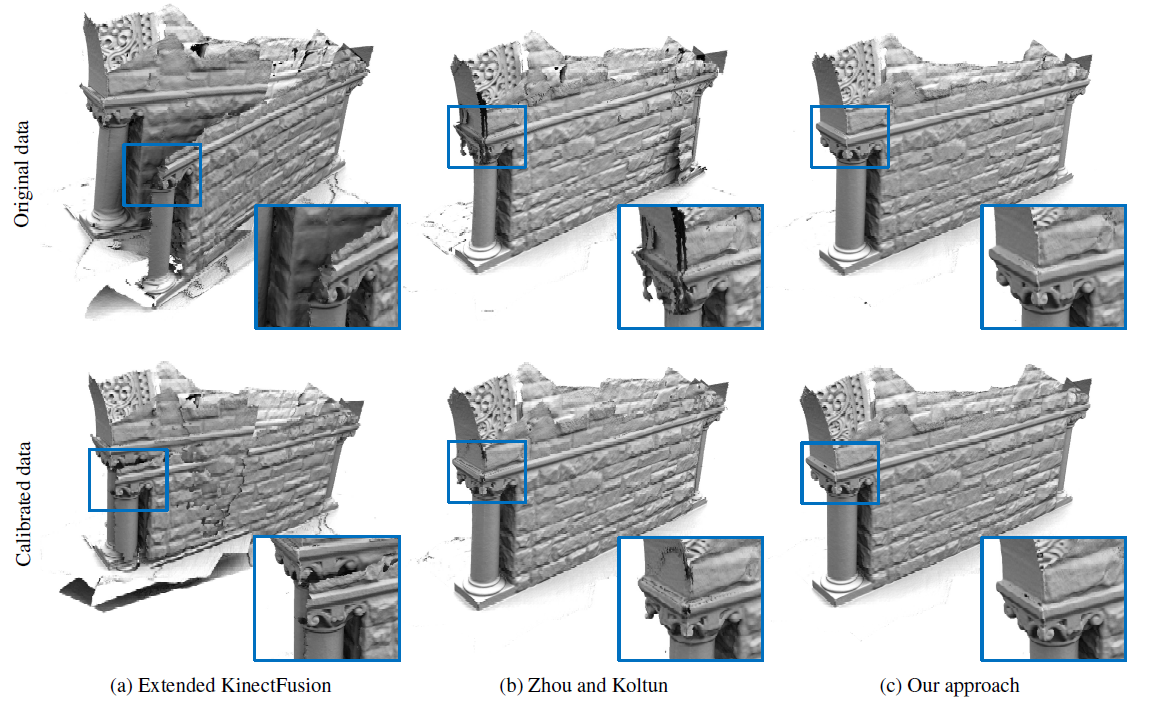
上图中第一列显示的是没有经过矫正重建的结果,第二列显示的是通过矫正后重建的结果,也可以看出,矫正可以降低 low-frequency distortion。
(a)列是 Extended KinectFusion 重建的结果,(b)列是“Dense Scene Reconstruction with Points of Interest”重建的结果,(c)列是“Elastic Fragments for Dense Scene Reconstruction”重建的结果。作者文章也提到,对于使用消费级深度相机像 Kinect 扫描,因为相机自身的 low-frequency distortion error,即使估计出来的相机的位姿再精确,也没法把场景重建得很好,也就说刚体变换没法把 fragments 融合好,这篇文章提出的方法是基于非刚体变换,融合 fragments。
这篇文章的思路也是先重建的 fragments,然后再融合 fragments 重建完整的场景,对于 fragments 重建,fragments 间配准和上篇博客介绍的思路相同,这里不再介绍。
Elastic 配准
算法输入的是一堆重建的局部的 fragments,目的是要找到一个映射,将 fragments 中所有的点,映射到同一个坐标系,并且对齐融合成一个场景。
优化的损失函数如下:
这里每个 fragment 中的每个点都会有一个独立的待优化参数
其中
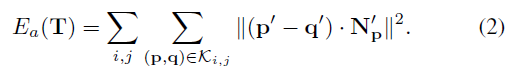
(2)式中,
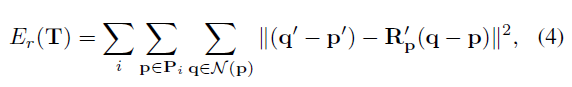
上式中,
可以看出待优化的参数个数和重建的点的个数成正比,实际操作的时候是不可行的,作者又给出了如下算法减少优化参数的个数。
作者对于在每个 fragment 中抽取控制点,fragment 中的其它点可以通过控制点插值得到,这时待优化的参数的个数就只和控制点的个数有关。但是,还有个问题是,这时优化的参数的个数和 fragment 的个数成正比关系,这在轨迹比较长的时候优化也是比较耗时的,下面介绍的 zhou 的另一篇文章可以解决这个问题。
这篇文章的思路和上篇文章有些类似,所以放在一起讲。前面说到 “Elastic Fragments for Dense Scene Reconstruction”中用优化抽取的控制点的变换来代替优化全部点变换,控制点比较稀疏,从而可以减少待优化的个数,但是“Elastic Fragments for Dense Scene Reconstruction”优化的参数个数还是和 fragments 的个数成正比关系。这篇文章的思路是在消畸变,因为每个相机的畸变是固定的,我在相机视场内抽样控制点,其它点的参数通过控制点的参数插值得到,移动相机重建的时候,每个点用控制点的参数做变换去畸变,这样待优化的参数个数不再和 fragments 的个数成正比关系,只和在相机视场内选取的控制点的个数相关。
待优化的损失函数
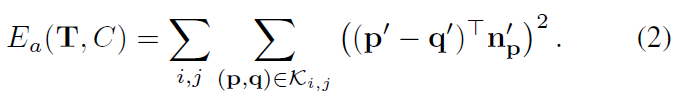
不同的是
其中
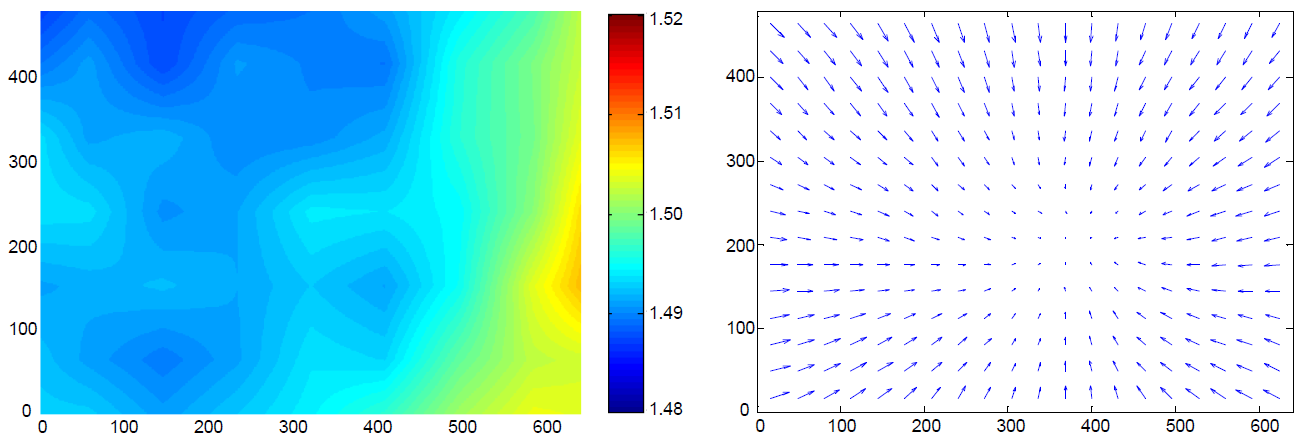
畸变矫正的表达式是通过相机视场内的点均匀抽样得到的,畸变矫正函数是一个 displacement field over the camera’s measuring volume,示意图如下:
因为损失函数
矫正函数正则项
- 上一篇: Golang: cobra
- 下一篇: C语言的基本数据类型总结