双数组字典树Double Array Trie（上）

本文转载自：http://www.cnblogs.com/zhangchaoyang 作者:Orisun 如有侵权，请联系本人，一定修改至您满意为止。

Trie树主要应用在信息检索领域，非常高效。今天我们讲Double Array Trie，请先把Trie树忘掉，把信息检索忘掉，我们来讲一个确定有限自动机（deterministic finite automaton ，DFA）的故事。所谓“确定有限自动机”是指给定一个状态和一个变量时，它能跳转到的下一个状态也就确定下来了，同时状态是有限的。请注意这里出现两个名词，一个是“状态”，一个是“变量”，下文会举例说明这两个名词的含义。

举个例子，假设我们一共有10个汉字，每个汉字就是一个“变量”。我们为每个汉字编个序号。

             表1. “变量”的编号

这10个汉字一共可以构成6个词语：啊，埃及，阿胶，阿根廷，阿拉伯，阿拉伯人。　　　　　　　　　

这里的每个词以及它的任意前缀都是一个“状态”，“状态”一共有10个：啊,阿,埃,阿根,阿根廷,阿胶,阿拉,阿拉伯,阿拉伯人,埃及

我们把DFA图画出来:

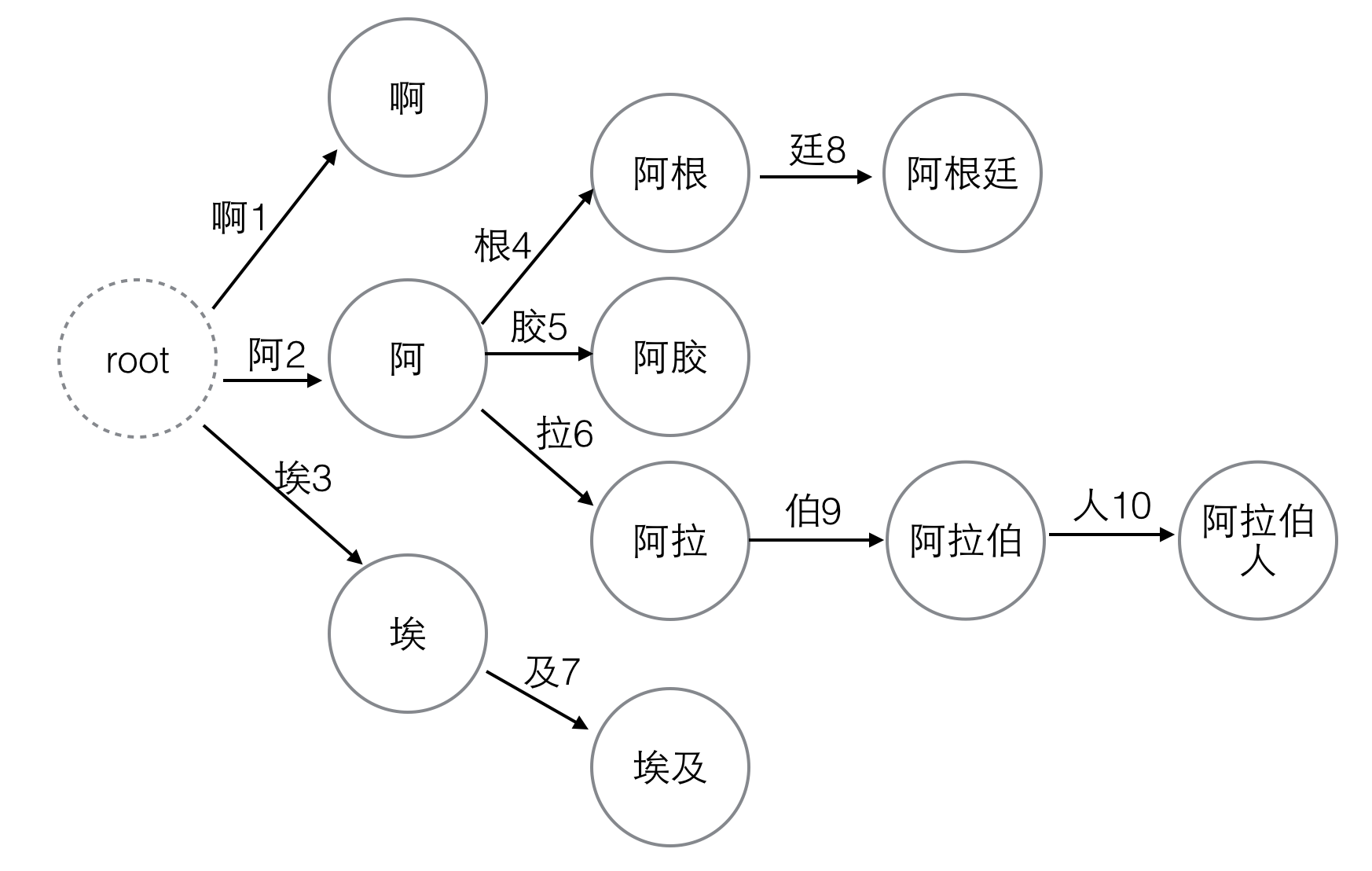
　　　　　　　　图1. DFA，同时也是Trie树

在图中每个节点代表一个“状态”，每条边代表一个“变量”，并且我们把变量的编号也标在了图中。

下面我们构造两个int数组：base和check，它们的长度始终是一样的。数组的长度定多少并没有严格的规定，反正随着词语的插入，数组肯定是要扩容的。说到数组扩容，大家可以看一下java中HashMap的扩容策略，每次扩容数组的长度都会变为2的整次幂。HashMap中有这么一个精妙的函数：

回到今天的正题，我们不妨把double array的初始长度就定得大一些。两数组元素初始值均为0。

double array的初始状态：

把词添加到词典的过程就给base和check数组中各元素赋值的过程。下面我们层次遍历图1所示的Trie树。

step1.

第一层上取到3个“状态”：啊,阿,埃。把这3个状态按照其对应的变量的编号（查表1）放到state数组中。